Reactions whose outcomes depend on dynamic processes is a major theme of my book and this blog. The recent study of the reaction of a nucleophile (hydroxide) with bromoacetophenones adds yet another case for post-transition state product determination.
Itoh and Yamataka have examined the reaction of hydroxide with substitutes α-bromoacetophenones 1.1 The nucleophile can attack at the carbonyl carbon or the α-carbon, though both lead ultimately to the same product, as shown in Scheme 1.
Scheme 1
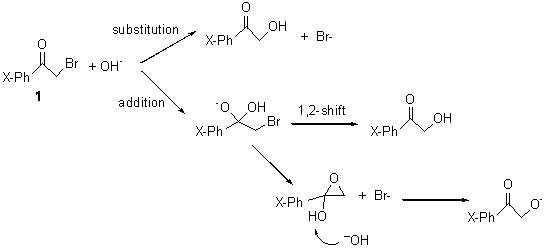
B3LYP/6-31+G* computations of the reaction surface with a variety of different substituents on the phenyl ring of 1 located in all cases a single transition state for the two different reactions (addition and substitution). This TS is shown in Figure 1 for the parent case (X=H).
Figure 1. The single transition state for the addition and substitution reaction of 1 and hydroxide.
Tracing the IRC forward leads to either the carbonyl addition product or the substitution product, and which path is traced depends to some extent on the nature of the substituent. Most intriguing is that trajectories initiated at the transition state lead to both products. So once again, we see a case where a single transition state leads to two products, and product selectivity is determine by the dynamics – the initial conditions at the TS dictate which of the two products is eventually obtained.
References
(1) Itoh, S.; Yoshimura, N.; Sato, M.; Yamataka, H., "Computational Study on the Reaction Pathway of α-Bromoacetophenones with Hydroxide Ion: Possible Path Bifurcation in the Addition/Substitution Mechanism," J. Org. Chem., 2011, 70, 8294–8299, DOI: 10.1021/jo201485y


Henry Rzepa responded on 25 Oct 2011 at 1:52 am #
I am not convinced this study is realistic. I checked the article, and no solvation correction appeared to have been made, with either explicit or continuum water molecules. This DOES make a big difference. For example, the simple SN1/SN2 hydrolysis of t-butyl chloride requires both explicit and implicit solvent (see the IRC for this process here) to produce what I would term a realistic result (i.e. one which can be compared with reasonable experiments). Whilst an IRC is only partially dynamic, and other processes are not part of the simulation (such as proton transfers), I firmly believe that ALL mechanistic studies of reactions which occur in condensed phases such as solution should nowadays be studied with solvation applied. Or if it is not, we should be informed of the appropriate gas phase experiments which provide the reality checks.
Henry Rzepa responded on 25 Oct 2011 at 9:50 am #
A nice example of a reaction with such a valley ridge inflexion point is the cyclodimerisation of cylopentadiene, although in this case the first transition state leads not to product but directly to a second transition state, from which two product outcomes are then possible. In fact, two IRCs are needed to fully describe this process.
Steven Bachrach responded on 25 Oct 2011 at 1:05 pm #
I agree that the omission of solvent is key in terms of comparing this to the most likely application of this chemistry – solution phase reactions. However, I blogged about this paper to demonstrate just how widespread are the examples of unusual potential energy surfaces and the need for dynamics – even in case that seem truly ordinary.
Henry Rzepa responded on 25 Oct 2011 at 2:09 pm #
If the potential energy surface is unrealistic, there might be little point in performing dynamics, since any “unusual” aspect of a potential energy surface could arise purely because of the approximations made rather than any reflection upon reality.
Steven Bachrach responded on 25 Oct 2011 at 2:17 pm #
True, and I agree that the PES provided here is unlikely to bear much resemblance to the solution phase PES. But there is no reason to believe that the computed PES is unreasonable for a gas phase reaction, and the gas phase dynamics are interesting on this unusual surface.
ITOH Shuhei responded on 25 Oct 2011 at 6:44 pm #
Sorry to say poor English.
The SN1 mechanism is generated a cation and anion. In this case, solvation is the a very important. On the other hand, the SN2 process does not generate a charge. In this case, solvation is a little important than SN1. Also, addtion/substitution mechanism does not generate a charge.
However, I understand need to the solvation. In this system, the solvent coordinate a hydroxide ion and another molecules. Implicit solvation models such as PCM are not best in this system. The FMO-MD or QM/MM MD simulations are necessary. But, I did not calculate this situation for computation costs.
The reaction of alpha-haloketons with nuculeophiles is studied for many years. The borderline case is found by difference of nucleophiles. Above all, borderline mechanism for alpha-haloketons with nuculeophiles is possible the path bifurcation.
And now, Prof. Yamataka is studing a experimint in solution phase.
Thank for discussion my study.
Henry Rzepa responded on 25 Oct 2011 at 9:41 pm #
Thanks Dr Shuhei for the interesting comments! I agree that for highly ionic systems, a hybrid model which includes explicit solvent (water) molecules is essential, contributing probably at least half of the solvation energy. They do make a difference, for example my model for the hydrolysis of t-butyl chloride with water looks very different when 16 water molecules (+ continuum solvent) are included. In this case of course, charge is generated, and solvent bridges form!
As a matter of interest, I took the coordinates for your model with R=H and tried to re-optimize with a continuum solvent applied (water). No transition state for the reaction could be found in the vicinity of the original coordinates, and we must presume it (and the potential) is changed quite a lot.
ITOH Shuhei responded on 26 Oct 2011 at 6:47 am #
I do not personally believe the continuum solvent methods and including some solvent molecular system. The continuum solvent methods is not including in the coordinated solvent. There is too many coordinated form of solvent in hybrid models. It is difficult to estimate to entropy factor, the most stable structure and metastable structures. Thus, I did not try the these methods for calculating in my system.
But, your results is a serious problem in my system. I try to calculate with a continuum solvent model. I need some more time to calculate. The results is obtained. Then, I am going to sent a e-mail to you.
Thank you for suggestion in the solvent effect.
Henry Rzepa responded on 26 Oct 2011 at 9:22 am #
My calculation can be found at DOI: 10042/to-9566. You will see it is a transition state, with a normal mode that is mostly the OH hydrogen wagging, and not perhaps the SN2/nucleophilic addition that is wanted. But an IRC would clarify this (I have not done that calculation).
Henry Rzepa responded on 27 Oct 2011 at 1:17 am #
The topologies of potential energy surfaces and of electron density ρ have interesting analogies. In both, features can “annihilate” each other (such as bond and ring critical points in ρ). Thus a reaction with two closely adjacent valleys may each have a saddle point order 1, or they may merge to form valley ridges, where one transition state leads directly to another.
I saw a lecture, perhaps 3 years ago, by someone who had spent years analysing the topological features of potential energy surfaces. As I remember, it had very unusual, even esoteric forms which take these concepts very much further, and terminologies to match! If only I could remember who he was (from France I think?). Can anyone help? The potentials by the way were generated analytically, and not from QM calculations.
Henry Rzepa responded on 28 Oct 2011 at 1:05 am #
I think I have found the person I mentioned above: Wolfgang Quapp. Articles by him include 10.1016/j.molstruc.2003.10.034 (2004, How does a reaction path branching take place? A classification of bifurcation events) and 10.1007/s00214-010-0749-z (2011, An empirical, variational method of approach to unsymmetric valley-ridge inflection points).
ITOH Shuhei responded on 28 Oct 2011 at 4:49 am #
Thank prof. Rzepa for updating of a transition structure. Though I am still in midst of the calculating, The TS of OH hydrogen wagging seems to be a TS of nucleophilic attack which is a only TS for nucleophilic attack according to scan(C(=O)-O(H) bond) , IRC(It goes to cmp-H) and energy of TS(TSnu-H > TSre-H). Now, I calculate reverse IRC now.
ITOH Shuhei responded on 20 Dec 2011 at 6:13 am #
Sorry it tooks so long. The results of IRC(algorithm is DVV) at The TS of OH hydrogen wagging reached substitution product. The results is same as that of vacuum.
Thus, the fact of bifurcation is similar between vacuum and PCM.
Thanks for suggestion.