Singleton has again found a great example of a simple reaction that displays unmistakable non-statistical behavior.¹ The hydroboration of terminal alkenes proceeds with selectivity, preferentially giving the anti-Markovnikov product. The explanation for this selectivity is given in all entry-level organic textbooks – who would think that such a simple reaction could in fact be extraordinarily complex?

Reaction 1, designed to minimize the role of hydroboration involving higher order boron-hydrides (RBH₂ and R₂BH), the ratio of anti-Markovnikov to Markovinkov product is 90:10. Assuming that this ratio derives from the difference in the transition state energies leading to the two products, using transition state theory gives an estimate of the energy difference of the two activation barriers of 1.1 to 1.3 kcal mol^-1.

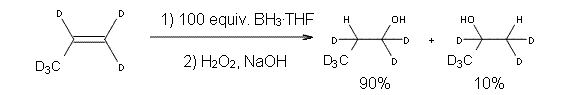
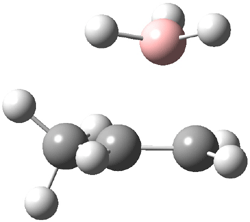
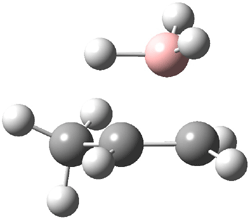
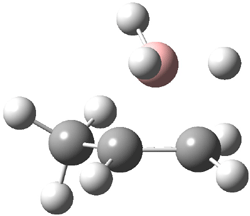
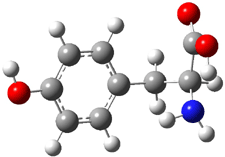
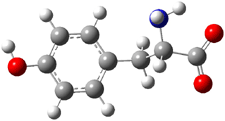
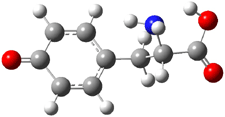
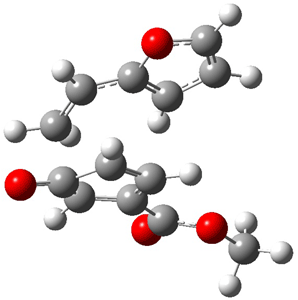
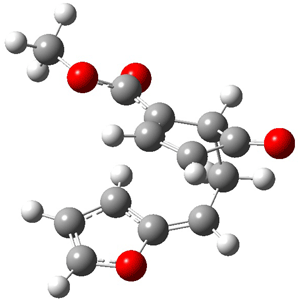
The CCSD(T)/aug-cc-pVDZ optimized structures of the precomplex between BH₃ and propene 1, along with the anti-Markovnikov transition state 2 and the Markovnikov transition state 3 are shown in Figure 2. The CCSD(T) energy extrapolated for infinite basis sets and corrected for enthalpy indicate that the difference between 2 and 3 is 2.5 kcal mol^-1. Therefore, transiitn state theory using this energy difference predicts a much greater selectivity of the anti-Markovnikov product, of about 99:1, than is observed.

1
2	3

Figure 1. CCSD(T)/aug-cc-pVDZ optimized geometries of 1-3.¹

In the gas phase, formation of the precomplex is exothermic and enthalpically barrierless. (A free energy barrier for forming the complex exists in the gas phase.) When a single THF molecule is included in the computations, the precomplex is formed after passing through a barrier much higher than the energy difference between 1 and either of the two transition states 2 or 3. (2 is only 0.8 kcal mol^-1 above 1 in terms of free energy.) So, Singleton speculated that there would be little residence time within the basin associated with 1 and the reaction might express non-statistical behavior.

Classical trajectories were computed. When trajectories were started at the precomplex 1, only 1% led to the Markovnikov product, consistent with transition state theory, but inconsistent with experiment. When trajectories were initiated at the free energy transition state for formation of the complex (either with our without a single complexed THF), 10% of the trajectories ended up at the Markovnikov product, as Singleton put it “fitting strikingly well with experiment”!

Hydroboration does not follow the textbook mechanism which relies on transition state theory. Rather, the reaction is under dynamic control. This new picture is in fact much more consistent with other experimental observations, like little change in selectivity with varying alkene substitution² and the very small H/D isotope effect of 1.18.³ Singleton adds another interesting experimental fact that does not jibe with the classical mechanism: the selectivity is little affect by temperature, showing 10% Markovnikov product at 21 °C and 11.2% Markovnikov product at 70 °C. Dynamic effect rears its ugly complication again!

References

(1) Oyola, Y.; Singleton, D. A., “Dynamics and the Failure of Transition State Theory in Alkene Hydroboration,” J. Am. Chem. Soc. 2009, 131, 3130-3131, DOI: 10.1021/ja807666d.

(2) Brown, H. C.; Moerikofer, A. W., “Hydroboration. XV. The Influence of Structure on the Relative Rates of Hydroboration of Representative Unsaturated Hydrocarbons with Diborane and with Bis-(3-methyl-2-butyl)-borane,” J. Am. Chem. Soc. 1963, 85, 2063-2065, DOI: 10.1021/ja00897a008.

(3) Pasto, D. J.; Lepeska, B.; Cheng, T. C., “Transfer reactions involving boron. XXIV. Measurement of the kinetics and activation parameters for the hydroboration of tetramethylethylene and measurement of isotope effects in the hydroboration of alkenes,” J. Am. Chem. Soc. 1972, 94, 6083-6090, DOI: 10.1021/ja00772a024.

Molecular structures can differ depending on phase, particularly between the gas and solution phase. Kass has looked at the protonation of 4-aminobenzoic acid. In water, the amino is its most basic site, but what is it in the gas phase? The computed relative energies of the protonation sites are listed in Table 1. If one corrects the B3LYP values for their errors in predicting the proton affinity of aniline and benzoic acid, the carbonyl oxygen is predicted to be the most basic site by 5.0 kcal mol^-1, in nice accord with the G3 prediction of 4.1 kcal mol^-1. Clearly, the structure depends on the medium.

Table 1. Computed relative proton affinities (kcal mol^-1) of 4-aminobenzoic acid.

Electrospray of 4-aminobenzoic acid from 3:1 methanol/water and 1:1 acetonitrile/water solutions gave different CID spectra. H/D exchange confirmed that electrospray from the emthanol/water solution gave the oxygen protonated species while that from the acetonitrile/water solution gave the ammonium species.

References

(1) Tian, Z.; Kass, S. R., “Gas-Phase versus Liquid-Phase Structures by Electrospray Ionization Mass Spectrometry,” Angew. Chem. Int. Ed., 2009, 48, 1321-1323, DOI: 10.1002/anie.200805392.

InChIs

4-aminobenzoic acid: InChI=1/C7H7NO2/c8-6-3-1-5(2-4-6)7(9)10/h1-4H,8H2,(H,9,10)/f/h9H
InChIKey=ALYNCZNDIQEVRV-BGGKNDAXCD

What is the rate determining step in the Hajos-Parrish-Eder-Sauer-Wiechert reaction (reaction 1)? This basic question of the mechanism for the first example of the use of proline as a catalyst remains unanswered, though a recent paper by Meyer and Houk¹ does moves us forward.

Their ¹³C kinetic isotope effect study revealed that only the nucleophilic ketone (the carboyl of the butyl chain) experiences any significant effect, with a value of about 1.03. B3LYP/6-31G(d,p) computations of the three transition states shown below were performed for both the gas phase and solution using IEF-PCM. Calculations of the transition state for the formation of the C-C bond (TS3) predicts no kinetic isotope effect, indicating that it is not the rate limiting step, in conflict with previous² suggestions. The transition states for the formation of the carbinolamine (TS1) and formation of the iminium (TS2) both predict an isotope effect comparable with experiment. TS1 is about 3 kcal mol^-1 higher in energy than TS2. The authors conclude that a step prior to formation of the C-C is the rate limiting step of the Hajos-Parrish-Eder-Sauer-Wiechert reaction, but cannot discern between the two possibilities examined.

References

(1) Zhu, H.; Clemente, F. R.; Houk, K. N.; Meyer, M. P., "Rate Limiting Step Precedes C-C Bond Formation in the Archetypical Proline-Catalyzed Intramolecular Aldol Reaction," J. Am. Chem. Soc., 2009, 131, 1632-1633, DOI: 10.1021/ja806672y.

(2) Clemente, F. R.; Houk, K. N., "Computational Evidence for the Enamine
Mechanism of Intramolecular Aldol Reactions Catalyzed by Proline," Angew. Chem. Int. Ed., 2004, 43, 5766-5768, DOI: 10.1002/anie.200460916.

InChIs

2-methyl-2-(3-oxobutyl)cyclopentane-1,3-dione:
InChI=1/C10H14O3/c1-7(11)5-6-10(2)8(12)3-4-9(10)13/h3-6H2,1-2H3
InChIKey=OZBYSCPBJGAYMQ-UHFFFAOYAW

(3aS,7aS)-3a-hydroxy-7a-methyl-3,4,6,7-tetrahydro-2H-indene-1,5-dione:
InChI=1/C10H14O3/c1-9-4-2-7(11)6-10(9,13)5-3-8(9)12/h13H,2-6H2,1H3/t9-,10+/m1/s1
InChIKey=PUHCDQVSBDIJTM-ZJUUUORDBA

Following on their prediction that the thiol of cysteine¹ is more acidic than the carboxylic acid group (see this post), Kass has examined the acidity of tyrosine 1.² Which is more acidic: the hydroxyl (leading to the phenoxide 2) or the carboxyl (leading to the carboxylate 3) proton?

Kass optimized the structures of tyrosine and its two possible conjugate bases at B3LYP/aug-cc-pVDZ, shown in Figure 1, and also computed their energies at G3B3. 2 is predicted to be 0.2 kcal mol^-1 lower in energy than 3 at B3LYP and slightly more stable at G3B3 (0.5 kcal mol^-1). However, both computational methods underestimate the acidity of acetic acid more than that of phenol. When the deprotonation energies are corrected for this error, the phenolic proton is predicted to be 0.4 kcal mol^-1 more acidic than the carboxylate proton at B3LYP and 0.9 kcal mol^-1 more acidic at G3B3.

1
2	3

Figure 1. B3LYP/aug-cc-pVDZ optimized structures of tyrosine 1 and its two conjugate bases 2 and 3.²

Gas phase experiments indicate that deprotonation of tyrosine leads to a 70:30 mixture of the phenoxide to carboxylate anions. The computations are in nice agreement with this experiment. (A Boltzmann weighting of the computed lowest energy conformers makes only a small difference to the distribution relative to using simply the single lowest energy conformer.) This demonstrates once again the important role of solvent, since only the carboxylate anion is seen in aqueous solution.

References

(1) Tian, Z.; Pawlow, A.; Poutsma, J. C.; Kass, S. R., "Are Carboxyl Groups the Most Acidic Sites in Amino Acids? Gas-Phase Acidity, H/D Exchange Experiments, and Computations on Cysteine and Its Conjugate Base," J. Am. Chem. Soc., 2007, 129, 5403-5407, DOI: 10.1021/ja0666194.

(2) Tian, Z.; Wang, X.-B.; Wang, L.-S.; Kass, S. R., "Are Carboxyl Groups the Most Acidic Sites in Amino Acids? Gas-Phase Acidities, Photoelectron Spectra, and Computations on Tyrosine, p-Hydroxybenzoic Acid, and Their Conjugate Bases," J. Am. Chem. Soc., 2009, 131, 1174-1181, DOI: 10.1021/ja807982k.

InChIs

1: InChI=1/C9H11NO3/c10-8(9(12)13)5-6-1-3-7(11)4-2-6/h1-4,8,11H,5,10H2,(H,12,13)/t8-/m0/s1/f/h12H
InChIKey=OUYCCCASQSFEME-QAXLLPJCDY

2: InChI=1/C9H11NO3/c10-8(9(12)13)5-6-1-3-7(11)4-2-6/h1-4,8,11H,5,10H2,(H,12,13)/p-1/t8-/m0/s1/fC9H10NO3/q-1
InChIKey=OUYCCCASQSFEME-HVHKCMLZDU

3: InChI=1/C9H11NO3/c10-8(9(12)13)5-6-1-3-7(11)4-2-6/h1-4,8,11H,5,10H2,(H,12,13)/p-1/t8-/m0/s1/fC9H10NO3/h11h,12H/q-1
InChIKey=OUYCCCASQSFEME-XGYCJDCADS

I missed this when it came out, but Quast, Sander and Borden have made the very interesting non-Kekule diradical 1.¹

³1

The EPR spectra shows the characteristic six-line signal, with zero-field splitting parameters consistent with related triplet diradicals. The Curie-Weiss plot is linear from 4.6 to 22.9 K. These data suggest a triplet ground state. CASSCF(14,14)/6-31G* computations indicate that the triplet lies 8.5 kcal mol^-1 below the singlet. The optimized triplet geometry is shown in Figure 1. The triplet ground state is consistent with the Borden-Davidson rules for radicals.²

31

Figure 1. CASSCF(14,14)/6-31G* optimized structure of triplet 1.

References

(1) Quast, H.; Nudling, W.; Klemm, G.; Kirschfeld, A.; Neuhaus, P.; Sander, W.; Hrovat, D. A.; Borden, W. T., "A Perimidine-Derived Non-Kekule Triplet Diradical," J. Org. Chem. 2008, 73, 4956-4961, DOI: 10.1021/jo800589y.

(2) Borden, W. T.; Davidson, E. R., "Effects of electron repulsion in conjugated hydrocarbon diradicals," J. Am. Chem. Soc. 1977, 99, 4587-4594, DOI: 10.1021/ja00456a010.

InChIs

1: InChI=1/C20H27N3/c1-19(2,3)13-8-12-9-14(20(4,5)6)11-16-17(12)15(10-13)22-18(21-7)23-16/h8-11H,1-7H3,(H2,21,22,23)/f/h22-23H
InChIKey=XAKUHDACNAUAAB-PDJAEHLQCL

Here’s a nice example of the application of computed solvation energies in non-aqueous studies. Cramer and Truhlar have employed their latest SM8 technique, which is parameterized for organic solvents and for water, to estimate solvation energies in olive oil.¹ Now you may wonder why solvation in olive oil of all things? But the partitioning of molecules between water and olive oil has been shown to be a good predictor of lipophilicity and therefore bioavailability of drugs! The model works reasonably well in reproducing experimental solvation energies and partition coefficients. They do make the case that fluorine substitution which appears to improve solubility in organics,originates not to more favorable solvation in organic solvents (like olive oil) but rather that fluorine substitution dramatically decreases solubility in water.

References

(1) Chamberlin, A. C.; Levitt, D. G.; Cramer, C. J.; Truhlar, D. G., "Modeling Free Energies of Solvation in Olive Oil," Mol. Pharmaceutics, 2008, 5, 1064-1079, DOI: 10.1021/mp800059u

Malonaldehyde 1 possesses a very short intramolecular hydrogen bond. Its potential energy surface has two local minima (the two mirror image hydrogen-bonded structures) separated by a C_2v transition state. Schaefer reports a high-level computational study for the search for even shorter hydrogen bonds that might even lead to a single well on the PES.¹

The hydrogen bond distance is characterized by the non-bonding separation between the two oxygen atoms. Table 1 shows the O^…O distance for a number of substituted malonaldehydes computed at B3LYP/DZP++. Electron withdrawing groups on C₂ reduce the O^..O distance (see trend in 1 → 4). Electron donating groups on C₁ and C₃ also reduce this distance (see 5 and 6). Bulky substituents on the terminal carbons also reduce the O^…O distance (see 7). Combining all of these substituent effects in 8 leads to the very short O^…O distance of 2.380 Å.

Table 1. Distance (Å) between the two oxygen atoms and the barrier for hydrogen transfer of substituted malonaldehydes .¹

^aFocal point energy. ^bFocal point energy and corrected for zero-point vibrational energy.

A shorter O^…O distance might imply a smaller barrier for hydrogen transfer between the two oxygens. The structures of 8 and the transition state for its hydrogen transfer are shown in Figure 1. The energies of a number of substituted malonaldehydes were computed using the focal point method, and the barriers for hydrogen transfer are listed in Table 1. There is a nice correlation between the O^…O distance and the barrier height. The barrier for 8 is quite small, suggesting that with some bulkier substituents, the barrier might vanish altogether, leaving only a symmetric structure. In fact, the barrier appears to vanish when zero-point vibrational energies are included.

8

8TS

Figure 1. B3LYP/DZP++ optimized geometries of 8 and the transition state for hydrogen transfer 8TS.¹

References

(1) Hargis, J. C.; Evangelista, F. A.; Ingels, J. B.; Schaefer, H. F., "Short Intramolecular Hydrogen Bonds: Derivatives of Malonaldehyde with Symmetrical Substituents," J. Am. Chem. Soc., 2008, 130, 17471-17478, DOI: 10.1021/ja8060672.

InChIs

1: InChI=1/C3H4O2/c4-2-1-3-5/h1-4H/b2-1-
InChIKey=GMSHJLUJOABYOM-UPHRSURJBI

2: InChI=1/C4H3NO2/c5-1-4(2-6)3-7/h2-3,6H/b4-2-
InChIKey=BHYIQMFSOGUTRT-RQOWECAXBC

3: InChI=1/C3H3NO4/c5-1-3(2-6)4(7)8/h1-2,5H/b3-1+
InChIKey=JBBHDCMVSJADCE-HNQUOIGGBS

4: InChI=1/C3H5BO2/c4-3(1-5)2-6/h1-2,5H,4H2/b3-1+
InChIKey=IQNKNZSFMBIPBI-HNQUOIGGBX

5: InChI=1/C3H6N2O2/c4-2(6)1-3(5)7/h1,6H,4H2,(H2,5,7)/b2-1-/f/h5H2
InChIKey=AOZIOAJNRYLOAH-KRHGAQEYDI

6: InChI=1/C5H8O4/c1-8-4(6)3-5(7)9-2/h3,6H,1-2H3/b4-3+
InChIKey=BYYYYPBUMVENKB-ONEGZZNKBI

7: InChI=1/C11H20O2/c1-10(2,3)8(12)7-9(13)11(4,5)6/h7,12H,1-6H3/b8-7-
InChIKey=SOZFXLUMSLXZFW-FPLPWBNLBX

8: InChI=1/C3H5N3O4/c4-2(7)1(3(5)8)6(9)10/h7H,4H2,(H2,5,8)/b2-1+/f/h5H2
InChIKey=IHYUFGCOUITNJP-CHFMFTGODK

Once again into the breach – how much strain can an aromatic species withstand and remain aromatic? Cyranski, Bodwell and Schleyer employ the [n](2,7)pyrenophanes 1 to explore this question.¹ As the tethering bridge gets shorter, the pyrene framework must pucker, presumably reducing its aromatic character. Systematic shrinking allows one to examine the loss of aromaticity as defined by aromatic stabilization energy (ASE), magnetic susceptibility exaltation (Λ) and NICS, among other measures.

They examined the series of pyrenophanes where the tethering chain has 6 to 12 carbon atoms. I have shown the structures of three of these compounds in Figure 1. The bend angle α is defined as the angle made between the outside ring plane and the horizon. Relative ASE is computed using Reaction 1, which cleverly avoids the complication of exactly (a) what is the ASE of pyrene itself and (b) what is the strain energy in these compounds.

1a	1d
1g

Figure 1. B3LYP/6-311G** optimized geometries of 1a, 1d, and 1g.¹

Reaction 1

The results of the computations for this series of pyrenophanes is given in Table 1. The bending angle smoothly increases with decreasing length of the tether. The ASE decreases in the same manner. The ASE correlates quite well with the bending angle, as does the relative magnetic susceptibility exaltation. The NICS(1) values become less negative with decreasing tether length.

Table 1. Computed values for the pyrenophanes.

All of these trends are consistent with reduced aromaticity with increased out-of-plane distortion of the pyrene framework. What may be surprising is the relatively small loss of aromaticity in this sequence. Even though the bend angle is as large as almost 40°, the loss of ASE is only 16 kcal mol^-1, only about a quarter of the ASE of pyrene itself. Apparently, aromatic systems are fairly robust!

References

(1) Dobrowolski, M. A.; Cyranski, M. K.; Merner, B. L.; Bodwell, G. J.; Wu, J. I.; Schleyer, P. v. R.,
"Interplay of π-Electron Delocalization and Strain in [n](2,7)Pyrenophanes," J. Org. Chem., 2008, 73, 8001-8009, DOI: 10.1021/jo8014159

InChIs

1a: InChI=1/C22H20/c1-2-4-6-16-13-19-9-7-17-11-15(5-3-1)12-18-8-10-20(14-16)22(19)21(17)18/h7-14H,1-6H2
InChIKey=SJCYSWGQWCIONQ-UHFFFAOYAF

1b: InChI=1/C23H22/c1-2-4-6-16-12-18-8-10-20-14-17(7-5-3-1)15-21-11-9-19(13-16)22(18)23(20)21/h8-15H,1-7H2
InChIKey=VHVKAELFYUXZEM-UHFFFAOYAW

1c: InChI=1/C24H24/c1-2-4-6-8-18-15-21-11-9-19-13-17(7-5-3-1)14-20-10-12-22(16-18)24(21)23(19)20/h9-16H,1-8H2
InChIKey=HXPWDTNIUQNKLV-UHFFFAOYAQ

1d: InChI=1/C25H26/c1-2-4-6-8-18-14-20-10-12-22-16-19(9-7-5-3-1)17-23-13-11-21(15-18)24(20)25(22)23/h10-17H,1-9H2
InChIKey=DWYMZJZWMFVOIR-UHFFFAOYAM

1e: InChI=1/C26H28/c1-2-4-6-8-10-20-17-23-13-11-21-15-19(9-7-5-3-1)16-22-12-14-24(18-20)26(23)25(21)22/h11-18H,1-10H2
InChIKey=PZBADGOJPAEUIK-UHFFFAOYAZ

1f: InChI=1/C27H30/c1-2-4-6-8-10-20-16-22-12-14-24-18-21(11-9-7-5-3-1)19-25-15-13-23(17-20)26(22)27(24)25/h12-19H,1-11H2
InChIKey=YVZIXELCLJHDLW-UHFFFAOYAO

1g: InChI=1/C28H32/c1-2-4-6-8-10-12-22-19-25-15-13-23-17-21(11-9-7-5-3-1)18-24-14-16-26(20-22)28(25)27(23)24/h13-20H,1-12H2
InChIKey=QDAMLTATWKFTFB-UHFFFAOYAF

Pyrene: InChI=1/C16H10/c1-3-11-7-9-13-5-2-6-14-10-8-12(4-1)15(11)16(13)14/h1-10H
InChIKey=BBEAQIROQSPTKN-UHFFFAOYAB

4,9-dimethylenepyrene: InChI=1/C18H12/c1-11-9-13-5-4-8-16-12(2)10-14-6-3-7-15(11)17(14)18(13)16/h3-10H,1-2H2
InChIKey=XAAPFSHIUHWWCM-UHFFFAOYAM

Singleton has taken another foray into the murky arena of “dynamic effects”, this time with the aim of trying to provide some guidance towards making qualitative product predictions.¹ He has examined four different Diels-Alder reaction involving two diene species, each of which can act as either the diene or dienophile. I will discuss the results of two of these reactions, namely the reactions of 1 with 2 (Reaction 1) and 1 with 3 (Reaction 2).

In the experimental studies, Reaction 1 yields only 4, while reaction 2 yields both products in the ratio 6:7 = 1.6:1. Standard transition state theory would suggest that there are two different transition states for each reaction, one corresponding to the 4+2 reaction where 1 is the dienophile and the other TS has 1 as the dienophile. Then one would argue that in Reaction 1, the TS leading to 4 is much lower in energy than that leading to 5, and for Reaction 2, the TS state leading to 6 lies somewhat lower in energy than that leading to 7.

Now the interesting aspect of the potential energy surfaces for these two reactions is that there are only two transition states. The first corresponds to the Cope rearrangement between the two products (connecting 4 to 5 on the PES of Reaction 1 and 6 to 7 on the PES of Reaction 2). That leaves only one TS connecting reactants to products! These four TSs are displayed in Figure 1.

Reaction 1	Reaction 2
TS 12→45	TS 13→67
Cope TS 4→5	Cope TS 6→7

Figure 1. MPW1K/6-31+G** TSs on the PES of Reactions 1 and 2.¹

These transition states are “bispericyclic” (first recognized by Caramella²), having the characteristics of both possible Diels-Alder reactions, i.e. for Reaction 1 these are the [4π₁+2π₂] and [4π₂+2π₁]. What this implies is that the reactants come together, cross over a single transition states and then pass over a bifurcating surface where the lowest energy path (the IRC or reaction path) continues on to one product only. The second product, however, can be reached by passing over this same transition state and then following some other non-reaction path. This sort of surface is ripe for experiencing non-statistical behavior, or “dynamic effects”.

Trajectory studies were then performed to explore the product distributions. Starting from TS 12→45, 39 trajectories were followed: 28 ended with 4 and 10 ended with 5 while one trajectory recrossed the transition state. Isomerization of 5 into 4 is possible, and the predicted low barrier for this explains the sole observation of 4. For Reaction 2, of the 33 trajectories that originated at TS 13→67, 12 led to 6 and 19 led to 7. This distribution is consistent with the experimental product distribution of a slight excess of 7 over 6.

Once again we see here a relatively simple reaction whose product distribution is only interpretable using expensive trajectory computations, and the result leave little simplifying concepts to guide us in generalizing to other (related) systems. Singleton does provide two rules-of-thumb that may help prod us towards creating some sort of dynamic model. First, he notes that the geometry of the single transition state that “leads” to the two products can suggest the major product. The TS geometry can be “closer” to one product over the other. For example, in TS 12→45 the two forming C-C bonds that differentiate the two products are 2.95 and 2.99 Å, and the shorter distance corresponds to forming 4. In TS 13→67, the two C-C distances are 2.83 and 3.13 Å, with the shorter distance corresponding to forming 6. The second point has to do with the position of the second TS, the one separating the two products. This TS acts to separate the PES into two basins, one for each product. The farther this TS is from the first TS, the greater the selectivity.

As Singleton notes, neither of these points is particularly surprising in hindsight. Nonetheless, since we have so little guidance in understanding reactions that are under dynamic control, any progress here is important.

References

(1) Thomas, J. B.; Waas, J. R.; Harmata, M.; Singleton, D. A., "Control Elements in Dynamically Determined Selectivity on a Bifurcating Surface," J. Am. Chem. Soc. 2008, 130, 14544-14555, DOI: 10.1021/ja802577v.

(2) Caramella, P.; Quadrelli, P.; Toma, L., "An Unexpected Bispericyclic Transition Structure Leading to 4+2 and 2+4 Cycloadducts in the Endo Dimerization of Cyclopentadiene," J. Am. Chem. Soc. 2002, 124, 1130-1131, DOI: 10.1021/ja016622h

InChIs

1: InChI=1/C7H6O3/c1-10-7(9)5-2-3-6(8)4-5/h2-4H,1H3
InChIKey=XDEAUYSKQHEYSC-UHFFFAOYAM

2: InChI=1/C8H12/c1-2-8-6-4-3-5-7-8/h2,6H,1,3-5,7H2
InChIKey=SDRZFSPCVYEJTP-UHFFFAOYAI

3: InChI=1/C6H6O/c1-2-6-4-3-5-7-6/h2-5H,1H2
InChIKey=QQBUHYQVKJQAOB-UHFFFAOYAO

4: InChI=1/C15H18O3/c1-18-14(17)15-9-8-13(16)12(15)7-6-10-4-2-3-5-11(10)15/h6,8-9,11-12H,2-5,7H2,1H3/t1,12-,15+/m1/s1
InChIKey=IASNDVSMFFVIFJ-GDHFLIHABF

5: InChI=1/C15H18O3/c1-18-15(17)13-8-11-10(7-12(13)14(11)16)9-5-3-2-4-6-9/h5,8,10-12H,2-4,6-7H2,1H3
InChIKey=XOFSMKQRRVWZHS-UHFFFAOYAW

6: InChI=1/C13H12O4/c1-16-13(15)10-6-8-7(5-9(10)12(8)14)11-3-2-4-17-11/h2-4,6-9H,5H2,1H3
InChIKey=HTSLDILNKGZMHE-UHFFFAOYAH

7: InChI=1/C13H12O4/c1-16-12(15)13-6-4-10(14)8(13)2-3-11-9(13)5-7-17-11/h3-9H,2H2,1H3/t8-,9?,13-/m1/s1
InChIKey=URYPWPBQFGUBGW-KEJGKJRFBM

Concern about the use of DFT for general use in organic chemistry remains high; see my previous posts (1, 2, 3). Houk has now examined the reaction enthalpies of ten simple Diels-Alder reactions using a variety of functionals in the search for the root cause of the problem(s).¹

The ten reactions are listed in Scheme 1, and involve cyclic and acyclic dienes and either ethylene or acetylene as the dienophile. Table 1 lists the minimum and maximum deviation of the DFT enthalpies relative to the CBS-QB3 enthalpies (which are in excellent accord with experiment). Clearly, all of the DFT methods perform poorly, with significant errors in these simple reaction energies. The exception is the MO6-2X functional, whose errors are only slightly larger than that found with the SCS-MP2 method. Use of a larger basis set (6-311+G(2df,2p)) reduced errors only a small amount.

Table 1. Maximum, minimum and mean deviation of reaction enthalpies (kcal mol^-1) for the reactions in Scheme 1 using the 6-31+G(d,p) basis set.¹

In order to discern where the problem originates, they next explore the changes that occur in the Diels-Alder reaction: two π bonds are transformed into one σ and one π bond and the conjugation of the diene is lost, leading to (proto)branching in the product. Reactions 1-3 are used to assess the energy consequence of converting a π bond into a σ bond, creating a protobranch, and the loss of conjugation, respectively.

The energies of these reactions were then evaluated with the various functionals. It is only with the conversion of the π bond into a σ bond that they find a significant discrepancy between the DFT estimates and the CBS-QB3 estimate. DFT methods overestimate the energy for the π → σ exchange, by typically around 5 kcal mol^-1, but it can be much worse. Relying on cancellation of errors to save the day for DFT will not work when these types of bond changes are involved. Once again, the user of DFT is severely cautioned!

References

(1) Pieniazek, S. N.; Clemente, F. R.; Houk, K. N., "Sources of Error in DFT Computations of C-C Bond Formation Thermochemistries: π → σ Transformations and Error Cancellation by DFT Methods," Angew. Chem. Int. Ed. 2008, 47, 7746-7749, DOI: 10.1002/anie.200801843