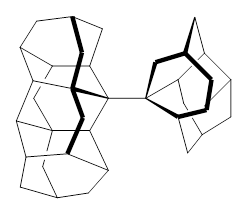
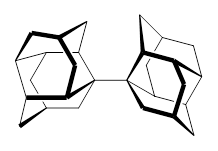
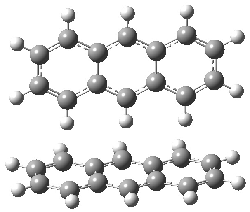
Schreiner has expanded on his previous paper¹ regarding alkanes with very long C-C bonds, which I commented upon in this post. He and his colleagues report² now a series of additional diamond-like and adamantane-like sterically congested alkanes that are stable despite have C-C bonds that are longer that 1.7 Å (such as 1! In addition they examine the structures and rotational barriers using a variety of density functionals.

For 2, the experimental C-C distance is 1.647 Å. A variety of functionals all using the cc-pVDZ basis predict distances that are much too long: B3LYP, B96, B97D, and B3PW91. However, functionals that incorporate some dispersion, either through an explicit dispersion correction (Like B3LYP-D and B2PLYP-D) or with a functional that address mid-range or long range correlation (like M06-2x) or both (like ωB97X-D) all provide very good estimates of this distance.

On the other hand, prediction of the rotational barrier about the central C-C bond of 2 shows different functional performance. The experimental barrier, determined by ¹H and ¹³C NMR is 16.0 ± 1.3 kcal mol^-1. M06-2x, ωB97X-D and B3LYP-D, all of which predict the correct C-C distance, overestimate the barrier by 2.5 to 3.5 kcal mol^-1, outside of the error range. The functionals that do the best in getting the rotational barrier include B96, B97D and PBE1PBE and B3PW91. Experiments and computations of the rotational barriers of the other sterically congested alkanes reveals some interesting dynamics, particularly that partial rotations are possible by crossing lower barrier and interconverting some conformers, but full rotation requires passage over some very high barriers.

In the closing portion of the paper, they discuss the possibility of very long “bonds”. For example, imagine a large diamond-like fragment. Remove a hydrogen atom from an interior position, forming a radical. Bring two of these radicals together, and their computed attraction is 27 kcal mol^-1 despite a separation of the radical centers of more than 4 Å. Is this a “chemical bond”? What else might we want to call it?

A closely related chemical system was the subject of yet another paper³ by Schreiner (this time in collaboration with Grimme) on the hexaphenylethane problem. I missed this paper somehow near
the end of last year, but it is definitely worth taking a look at. (I should point out that this paper was already discussed in a post in the Computational Chemistry Highlights blog, a blog that acts as a journals overlay – and one I participate in as well.)

So, the problem that Grimme and Schreiner³ address is the following: hexaphenylethane 3 is not stable, and 4 is also not stable. The standard argument for their instabilities has been that they are simply too sterically congested about the central C-C bond. However, 5 is stable and its crystal structure has been reported. The central C-C bond length is long: 1.67 Å. But why should 5 exist? It appears to be even more crowded that either 3 or 4. TPSS/TZV(2d,2p) computations on these three compounds indicate that separation into the two radical fragments is very exoergonic. However, when the “D3” dispersion correction is included, 3 and 4 remain unstable relative to their diradical fragments, but 5 is stable by 13.7 kcal mol^-1. In fact, when the dispersion correction is left off of the t-butyl groups, 5 becomes unstable. This is a great example of a compound whose stability rests with dispersion attractions.

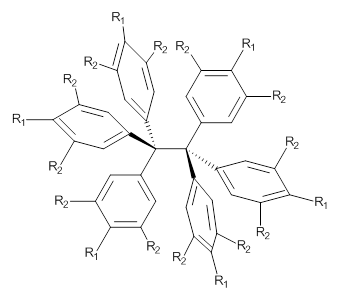
3: R₁ = R₂ = H
4: R₁ = tBu, R₂ = H
5: R₁ = H, R₂ = tBu

References

(1) Schreiner, P. R.; Chernish, L. V.; Gunchenko, P. A.; Tikhonchuk, E. Y.; Hausmann, H.; Serafin, M.; Schlecht, S.; Dahl, J. E. P.; Carlson, R. M. K.; Fokin, A. A. "Overcoming lability of extremely long alkane carbon-carbon bonds through dispersion forces," Nature 2011, 477, 308-311, DOI: 10.1038/nature10367

(2) Fokin, A. A.; Chernish, L. V.; Gunchenko, P. A.; Tikhonchuk, E. Y.; Hausmann, H.; Serafin, M.; Dahl, J. E. P.; Carlson, R. M. K.; Schreiner, P. R. "Stable Alkanes Containing Very Long Carbon–Carbon Bonds," J. Am. Chem. Soc., 2012, 134, 13641-13650, DOI: 10.1021/ja302258q

(3) Grimme, S.; Schreiner, P. R. "Steric Crowding Can tabilize a Labile Molecule: Solving the Hexaphenylethane Riddle," Angew. Chem. Int. Ed., 2011, 50, 12639-12642, DOI: 10.1002/anie.201103615

For those of you interested in learning about dispersion corrections for density functional theory, I recommend Grimme’s latest review article.¹ He discusses four different approaches to dealing with dispersion: (a) vdW-DF methods whereby a non-local dispersion term is included explicitly in the functional, (b) parameterized functional which account for some dispersion (like the M06-2x functional), (c) semiclassical corrections, labeled typically as DFT-D, which add an atom-pair term that typically has an r^-6 form, and (d) one-electron corrections.

The heart of the review is the comparison of the effect of including dispersion on thermochemistry. Grimme nicely points out that reaction energies and activation barriers typically are predicted with errors of 6-8 kcal mol^-1 with conventional DFT, and these errors are reduced by up to 1.5 kcal mol^-1 with the inclusion fo the “-D3” correction. Even double hybrid methods, whose mean errors are much smaller (about 3 kcal mol^-1), can be improved by over 0.5 kcal mol^-1 with the inclusion of the “-D3” correction. The same is also true for conformational energies.

Since the added expense of including the “-D3” correction is small, there is really no good reason for not including it routinely in all types of computations.

(As an aside, the article cited here is available for free through the end of this year. This new journal WIREs Computational Molecular Science has many review articles that will be of interest to readers of this blog.)

References

(1) Grimme, S., "Density functional theory with London dispersion corrections," WIREs Comput. Mol. Sci., 2011, 1, 211-228, DOI: 10.1002/wcms.30

The much publicized failure of common DFT methods to accurately describe alkane isomer energy and bond separation reactions (which I have blogged about many times) has recently been attributed to long-range exchange¹ (see this post) or simply just DFT exchange² (see this post). Grimme now responds by emphatically claiming that it is a failure in accounting for medium-range electron correlation.³

First, Grimme notes that the bond separation energy for linear alkanes (as defined in
Reaction 1) is underestimated by HF, and slightly overestimated by MP2, but SCS-MP2 provides energy in nice agreement with CCSD(T)/CBS energies. Since MP2 adds in coulomb correlation to the HF energy (which treats exchange exactly within a one determinant wavefunction), the traditional wavefunction approach strongly suggests a correlation error.

CH₃(CH₂)_mCH₃ + mCH₄ → (m+1)CH₃CH₃        Reaction 1

Next, bond separation energies computed with PBE and BLYP (which lack exact exchange), PBE0 (which has 25% non-local exchange) and BHLYP (which has 50% non-local exchange) are all similar and systematically too small. So, exchange cannot be the culprit. It must be correlation.

He also makes two other interesting points. First, inclusion of a long-range correction – his recently proposed D3 method⁴ – significantly improves results, but the bond separation energies are still underestimated. It is only with the double-hybrid functional B2PLYP and B2GPPLYP that very good bond separation energies are obtained. And these methods do address the medium-range correlation issue. Lastly, Grimme notes that use of zero-point vibrational energy corrected values or enthalpies based on a single conformation are problematic, especially as the alkanes become large. Anharmonic corrections become critical as does inclusion of multiple conformations with increasing size of the molecules.

References

(1) Song, J.-W.; Tsuneda, T.; Sato, T.; Hirao, K., "Calculations of Alkane Energies Using Long-Range Corrected DFT Combined with Intramolecular van der Waals Correlation," Org. Lett., 2010, 12, 1440–1443, DOI: 10.1021/ol100082z

(2) Brittain, D. R. B.; Lin, C. Y.; Gilbert, A. T. B.; Izgorodina, E. I.; Gill, P. M. W.; Coote, M. L., "The role of exchange in systematic DFT errors for some organic reactions," Phys. Chem. Chem. Phys., 2009, DOI: 10.1039/b818412g.

(3) Grimme, S., "n-Alkane Isodesmic Reaction Energy Errors in Density Functional Theory Are Due to Electron Correlation Effects," Org. Lett. 2010, 12, 4670–4673, DOI: 10.1021/ol1016417

(4) Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H., "A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu," J. Chem. Phys., 2010, 132, 154104, DOI: 10.1063/1.3382344.

Back when I was first learning ab initio methods in Cliff Dykstra’s lab, I played a bit with the post-HF method CEPA (couple electron pair approximation). This method fell out of favor over the years with the rise of MP theory and then with DFT. Now, Neese and Grimme and co-workers are resurrecting it.¹ Their Accounts article provides a series of tests of CEPA/1 against benchmark computations (typically CCSD(T)) and lo and behold, CEPA performs remarkably well! It bests B3LYP (no surprise there), B2LYP and MP2 in virtually every category, ranging from reaction energies, hydrogen bond energies, van der Waals interaction energies, and activation barrier heights. As an example, for the isomerization energy of toluene to norbornadiene, CCSD(T) estimates the energy is 42.79 kcal mol^-1. B3LYP does miserably, with an error of nearly 14 kcal mol^-1, but the CEPA/1 estimate is off by only 0.04 kcal mol^-1. Since the computational time of CEPA/1 is competitive with MP2, the authors conclude that CEPA/1 is well-worth reinvestigating as an alternative post-HF methodology.

References

(1) Neese, F.; Hansen, A.; Wennmohs, F.; Grimme, S., "Accurate Theoretical Chemistry with Coupled Pair Models," Acc. Chem. Res. 2009, 42, 641-648 DOI: 10.1021/ar800241t.

I blogged on Bickelhaput’s examination of the stability of kinked vs. linear polycyclic aromatics¹ in this post. Bickelhaupt argued against any H^…H stabilization across the bay region, a stabilization that Matta and Bader² argued is present based on the fact that there is a bond path linking the two hydrogens.

Grimme and Erker have now added to this story.³ They prepared the dideuterated phenanthrene 1 and obtained its IR and Raman spectra. The splitting of the symmetric (a₁) and asymmetric (b₁) vibrational frequencies is very small 9-12 cm^-1. The computed splitting are in the same range, with very small variation with the computational methodology employed. The small splitting argues against any significant interaction between the two hydrogen (deuterium) atoms. Further, the sign of the coupling between the two vibrations indicates a repulsive interaction between the two atoms. These authors argue that the vibrational splitting is almost entirely due to conventional weak van der Waals interactions, and that there is no “bond” between the two atoms, despite the fact that a bond path connects them. This bond path results simply from two (electron density) basins forced to butt against each other by the geometry of the molecule as a whole.

References

(1) Poater, J.; Visser, R.; Sola, M.; Bickelhaupt, F. M., "Polycyclic Benzenoids: Why Kinked is More Stable than Straight," J. Org. Chem. 2007, 72, 1134-1142, DOI: 10.1021/jo061637p

(2) Matta, C. F.; Hernández-Trujillo, J.; Tang, T.-H.; Bader, R. F. W., "Hydrogen-Hydrogen Bonding: A Stabilizing Interaction in Molecules and Crystals," Chem. Eur. J. 2003, 9, 1940-1951, DOI: 10.1002/chem.200204626

(3) Grimme, S.; Mück-Lichtenfeld, C.; Erker, G.; Kehr, G.; Wang, H.; Beckers, H. W., H., "When Do Interacting Atoms Form a Chemical Bond? Spectroscopic Measurements and Theoretical Analyses of Dideuteriophenanthrene," Angew. Chem. Int. Ed. 2009, 48, 2592-2595, DOI: 10.1002/anie.200805751

InChIs

1: InChI=1/C14H10/c1-3-7-13-11(5-1)9-10-12-6-2-4-8-14(12)13/h1-10H/i7D,8D
InChIKey=YNPNZTXNASCQKK-QTQOOCSTEC

Another two benchmarking studies of the performance of DFT have appeared.

The first is an examination by Csonka and French of the ability of DFT to predict the relative energy of carbohydrate conformation energies.¹ They examined 15 conformers of α- and β-D-allopyranose, fifteen conformations of 3,6-anydro-4-O-methyl-D-galactitol and four conformers of β-D-glucopyranose. The energies were referenced against those obtained at MP2/a-cc-pVTZ(-f)//B3LYP/6-31+G*. (This unusual basis set lacks the f functions on heavy atoms and d and diffuse functions on H.) Among the many comparisons and conclusions are the following: B3LYP is not the best functional for the sugars, in fact all other tested hybrid functional did better, with MO5-2X giving the best results. They suggest the MO5-2X/6-311+G**//MO5-2x/6-31+G* is the preferred model for sugars, except for evaluating the difference between ¹C₄ and ⁴C₁ conformers, where they opt for PBE/6-31+G**.

The second, by Korth and Grimme, describes a “mindless” DFT benchmarking study.²
This is really not a “mindless” study (as the term is used by Schaefer and Schleyer³ and discussed in this post, where all searching is done in a totally automated way) but rather Grimme describes a procedure for removing biases in the test set. Selection of “artificial molecules” is made by first deciding how many atoms are to be present and what will be the distribution of elements. In their two samples, they select systems having 8 atoms. The two sets differ by the distribution of the elements. The first set the atoms Na-Cl are one-third as probable as the elements Li-F, which are one-third as probable as H. The second set has the probability distribution similar to those found in naturally occurring organic compounds. The eight atoms, randomly selected by the computer, are placed in the corners of a cube and allowed to optimize (this is reminiscent of the “mindless” procedure of Schaefer and Schleyer³). This process generates a selection of random bonding environments along with open- and closed shell species, and removes (to a large degree) the biases of previous test sets, which are often skewed towards small molecules, ones where accurate experiments are available or geared towards a select group of molecules of interest. Energies are then computed using a variety of functional and compared to the energy at CCSD(T)/CBS. The bottom line is that the functional nicely group along the rungs defined by Perdew:⁴ LDA is the poorest performer, GGA does much better, the third rung of meta-GGA functionals are slightly better than GGA functionals, hybrids do better still, and the fifth rung functionals (double hybrids) perform quite well. Also of interest is that CCSD(T)/cc-pVDZ gives quite large errors and so Grimme cautions against using this small basis set.

References

(1) Csonka, G. I.; French, A. D.; Johnson, G. P.; Stortz, C. A., "Evaluation of Density Functionals and Basis Sets for Carbohydrates," J. Chem. Theory Comput. 2009, ASAP, DOI: 10.1021/ct8004479.

(2) Korth, M.; Grimme, S., ""Mindless" DFT Benchmarking," J. Chem. Theory Comput. 2009, ASAP, DOI: 10.1021/ct800511q.

(3) Bera, P. P.; Sattelmeyer, K. W.; Saunders, M.; Schaefer, H. F.; Schleyer, P. v. R., "Mindless Chemistry," J. Phys. Chem. A 2006, 110, 4287-4290, DOI: 10.1021/jp057107z.

(4) Perdew, J. P.; Ruzsinszky, A.; Tao, J.; Staroverov, V. N.; Scuseria, G. E.; Csonka, G. I., "Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits," J. Chem. Phys. 2005, 123, 062201-9, DOI: 10.1063/1.1904565

The importance of the interactions between neighboring aromatic molecules cannot be overemphasized – π-π-stacking is invoked to explain the structure of DNA, the hydrophobic effect, molecular recognition, etc. Nonetheless, the nature of this interaction is not clear. In fact the commonly held notion of π-π orbital overlap is not seen in computations.

Grimme¹ has now carefully examined the nature of aromatic stacking by comparison with aliphatic analogues. He has examined dimers formed of benzene 1, naphthalene 2, anthracene 3, and teracene 4 and compared these with the dimers of their saturated analogues (cyclohexane 1s, decalin 2s, tetradecahydroanthracene 3s, and octadecahydrotetracene 4s. The aromatic dimmers were optimized in the T-shaped and stacked arrangements, and these are shown for 3 along with the dimer of 3s in Figure 1. These structures are optimized at B97-D/TZV(2d,2p) – a functional designed for van der Waals compounds. Energies were then computed at B2LYP-D/QZV3P, double-hybrid functional that works very well for large systems.

Figure 1. Optimized structures of 3s, 3t, and 3a.

The energies for formation of the complexes are listed in Table 1. The first interesting result here is that the benzene and naphthalene dimmers (whether stacked or T-shaped) are bound by about the same amount as their saturated analogues. Grimme thus warns that “caution is required to not overestimate the effect of the π system”.

Table 1. Complexation energy (kcal mol^-1)

The two larger aromatics here do show a significantly enhanced complexation energy than their saturated analogues, and Grimme refers to this extra stabilization as the π-π stacking effect (PSE). Energy decomposition analysis suggests that electrostatic interactions actually favor the complexation of the saturated analogues over the aromatics. However, Pauli exchange repulsion essentially cancels the electrostatic attraction for all the systems, and it is dispersion that accounts for the dimerization energy. Dispersion increases with size of the molecule, and “classical” dispersion forces (the R^-6 relationship) accounts for more than half of the dispersion energy in the saturated dimmers, while it is the non-classical, or orbital-based, dispersion that dominates in the stacked aromatic dimmers. Grimme attributes this to “special nonlocal electron correlations between the π electrons in the two fragments at small interplane distances”.

References

(1) Grimme, S., "Do Special Noncovalent π-π Stacking Interactions Really Exist?," Angew. Chem. Int. Ed., 2008, 47, 3430-3434, DOI: 10.1002/anie.200705157.

InChIs

1: InChI=1/C6H6/c1-2-4-6-5-3-1/h1-6H

1s: InChI=1/C6H12/c1-2-4-6-5-3-1/h1-6H2

2: InChI=1/C10H8/c1-2-6-10-8-4-3-7-9(10)5-1/h1-8H

2s: InChI=1/C10H18/c1-2-6-10-8-4-3-7-9(10)5-1/h9-10H,1-8H2

3: InChI=1/C14H10/c1-2-6-12-10-14-8-4-3-7-13(14)9-11(12)5-1/h1-10H

3s: InChI=1/C14H24/c1-2-6-12-10-14-8-4-3-7-13(14)9-11(12)5-1/h11-14H,1-10H2

4: InChI=1/C18H12/c1-2-6-14-10-18-12-16-8-4-3-7-15(16)11-17(18)9-13(14)5-1/h1-12H

4s: InChI=1/C18H30/c1-2-6-14-10-18-12-16-8-4-3-7-15(16)11-17(18)9-13(14)5-1/h13-18H,1-12H2