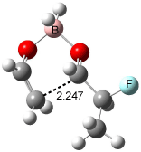The search for a stable molecule containing a hypercoordinated carbon atom may finally be over. Abboud and Yáñez¹ report mass spectra and computations on the unusual cation Si(CH₃)₃CH₃Si(CH₃)₃⁺ (1). Using low pressure FT-ICR, upon ionization of Si(CH₃)₄ (TMS) they observe a small signal with m/z 161.12, which corresponds to the mass of 1⁺. When Si(CH₃)₄ and Si(CD₃)₄ are mixed, introduced into the spectrometer and ionized, the mixed isotopomer of 1⁺ is observed, and scrambling to the CH₃ and CD₃ groups occurs.

The geometry of 1⁺ was optimized at B3LYP/6-311+G(3df,2pd) and QCISD/6-311+G(d,p). The latter structure is shown in Figure 1, though the geometry differs little between the two computations. The enthalpy for the dissociation of 1⁺ into TMS and Si(CH₃)₃⁺ is 23.2 kcal mol^-1 at QCISD. This compares very well with the experimental² value of 22.3 kcal mol^-1.

xyz file

Figure 1. QCISD/6-311+G(d,p) optimized structure of 1⁺.¹

The structure has C_3h symmetry with the central carbon to silicon distance of 2.071 Å, a bit more than a 10% increase over the length of a typical C-Si bond. Topological electron density analysis indicates a bond critical point does connect the central carbon atom with each silicon atom, and the value of the Laplacian of the electron density at this critical point is negative. This analysis strongly suggests that the central carbon atom is pentacoordinate!

Abboud and Yáñez argue that 1⁺ can be considered as a complex of methyl cation and two Si(CH₃)₃ radicals. The empty p orbital of the central methyl carbon can then interact with the radical-bearing orbital on each silicon, forming a three-center two-electron bonding molecular orbital (Scheme 1). The positive charge is delocalized, with the central methyl group having a charge of +0.26 while the charge on each Si(CH₃)₃ groups is +0.37.

Scheme 1.

Though not discussed in this paper, the all carbon analogue, namely C(CH₃)₃CH₃C(CH₃)₃⁺
is not a stable structure when restricted to have C_3h symmetry (see Figure 2). Rather, this geometry corresponds to the transition state for the transfer of a methyl group from one C(CH₃)₃ group to the other.

xyz files

Figure 1. B3LYP/6-311+G(d,p) optimized geometry of C(CH₃)₃CH₃C(CH₃)₃⁺.

References

(1) Daacute;valos, J. Z.; Herrero, R.; Abboud, J.-L. M.; Mó, O.; Yáñez, M., "How Can a Carbon Atom Be Covalently Bound to Five Ligands? The Case of Si₂(CH₃)₇⁺," Angew. Chem. Int. Ed. 2007, 46, 381-385, DOI: 10.1002/anie.200601164

(2) Wojtyniak, A. C. M.; Li, X.; Stone, J. A., "The Formation of CH₃)₇Si₂⁺ in (CH₃)₄Si/CH₄ Mixtures and CH₃−Exchange Reactions between (CH₃)₄Si, (CH₃)₄Ge, and (CH₃)₄Sn Studied by High Pressure Mass Spectrometry," Can. J. Chem. 1987, 65, 2849-2854,

In Chapter 1.6.2 we discuss computed NMR spectra, and in particular note some successes in correlating predicted chemical shifts with experiment values. Recently, Rychnovsky took the next logical step, utilizing computational methods to predict the NMR spectrum of a compound whose structure was in doubt.

Hexacyclinol was isolated from Panus Rudis, a type of mushroom. Based on spectroscopic studies, Gräfe proposed 1 as its structure.¹ Le Clair claimed to have synthesized a substance with this structure in 2006.² This article became a cause célèbre in the blogosphere,³ with serious doubts cast upon the veracity of the author and his claims.

Rychnovsky⁴ doubted that the molecule actually possessed the unusual structure of 1. Since the actual structure was unknown, he proposed to compute the NMR shifts based on the optimized structure of 1 and compare them with the experimental values. Given the very large size of hexacyclinol, the computational approach would have to be rather limited. Therefore, whatever (small) method was to be employed would have to be tested for adequate predictive performance with known compounds. Rychnovsky selected the three diterpenes elisapterosin B 2, elisabethin A 3, and maoecrystal V 4 to benchmark his computations. His computational approach was to first utilize a Monte Carlo search with the MMFF force field to identify low lying conformers. The best conformer was then optimized at HF/3-21G and the chemical shifts were computed using this geometry with the GIAO/mPW1PW91/6-31G(d,p). The optimized structures of the diterpenes 2-3 are shown in Figure 1.

elisapterosin B 2 xyz file PubChem entry
elisabethin A 3 xyz file
maoecrystal V 4 xyz file

Figure 1. HF/3-21G optimized structures of 2-3.⁴

The computed ¹³C chemical shifts for these test compounds were then plotted against the experimental values and a linear fit was determined to correct the computed values. The average ¹³C chemical shift difference between computation and experiment is less than 2 ppm, and no difference exceeds 5 ppm. Next, Rychnovsky optimized the proposed structure of hexacyclinol 1, shown in Figure 2, and computed its ¹³C chemical shifts and corrected them using the fitting procedure developed for the three test compounds. These computed chemical shifts were in poor agreement with the experimental values; the average deviation was 6.8 ppm and five shifts differ by more than 10 ppm. Rychnovsky concluded that this poor agreement discredits the proposed structure 1.

1
xyz file

Figure 2. HF/3-21G optimized structures of 1.⁴

As an alternative, Rychnovsky proposed that hexacyclinol is in fact the by-product from work-up of the natural product panepophenanthrin, also obtained from Panus rudis. He proposed that hexacylinol has the structure shown in 5. He optimized the geometry of 5 and obtained two low-energy conformers. The second-lowest conformer, shown in Figure 3, has a predicted ¹³C NMR spectrum in very close agreement with experiment. Its average chemical shift deviation is 1.8 ppm with a maximum difference of 5.8 ppm. These differences are consistent with those found in the diterpenes test set. This structure has now been synthesized by Porco and its x-ray structure obtained.⁵ This compound has the structure predicted by Rychnovsky and is completely consistent with the original hexacyclinol compound reported by Gräfe. This successful resolution of the structure of hexacycliinol should spur further use of computational methods to predict NMR spectra and evaluate chemical structures. ACD has recently applied its method for predicting NMR spectra to the problem of hexacylinol.⁶ You can read about this on the ChemSpider blog.

5 xyz file

Figure 3. HF/3-21G optimized structures of 5.⁴

References

(1) Schlegel, B.; Hartl, A.; Dahse, H.-M.; Gollmick, F. A.; Gräfe, U.; Dorfelt, H.; Kappes, B., “Hexacyclinol, a New Antiproliferative Metabolite of Panus Rudis HKI 0254,” J. Antibiot. 2002, 55, 814-817.

(2) La Clair, J. J., “Total Syntheses of Hexacyclinol, 5-epi-Hexacyclinol, and Desoxohexacyclinol Unveil an Antimalarial Prodrug Motif,” Angew. Chem. Int. Ed. 2006, 45, 2769-2773, DOI: 10.1002/anie.200504033

(3) (a) Halford, B., “Hexacyclinol Debate Heats Up,” Chem. Eng. News 2006, 84 (31, July 28), 11, http://pubs.acs.org/cen/news/84/i31/8431notw1.html. (b) Love, D. “Hexacyclinol? Or Not?” http://pipeline.corantte.com/archives/2006/06/05/hexacyclinol_or_not.php (c) “Structure Revision of Hexacyclinol”, http://totallynthetic.com/blog/?p=110 (d) Halford, B., “Hexacyclinol Showdown: The Biggest Non-Event at the ACS Meeting”, http://cenonline.blogs.com/sanfrancisco_2006/2006/09/hexacyclinol_sh.html (e) “Hexacyclinol Rides Again”, http://www.healthvoices.com/feed/items/blog_perspective/consultants/pharma/2006/07/3/hexacyclinol_rides_again

(4) Rychnovsky, S. D., “Predicting NMR Spectra by Computational Methods: Structure Revision of Hexacyclinol,” Org. Lett. 2006, 8, 2895-2898, DOI: 10.1021/ol0611346

(5) Porco, J. A. J.; Shun Su, S.; Lei, X.; Bardhan, S.; Rychnovsky, S. D., “Total Synthesis and Structure Assignment of (+)-Hexacyclinol,” Angew. Chem. Int. Ed. 2006, 45, 5790-5792, DOI: 10.1002/anie.200602854
(6) Elyashberg, M. E.; Williams, A. J.; Martin, G. E., “Computer-Assisted Structure Verification and Elucidation Tools in NMR-Based Structure Elucidation,” Prog. Nuc. Mag. Res. Spectrosc., 2007, in press, DOI: 10.1016/j.pnmrs.2007.04.003.

InChI

1: InChI=1/C23H28O7/c1-8(2)6-11-23-10(22(3,4)27-5)7-9-12(21(23)26)13-15(23)18(30-29-11)14(17(13)25)19-20(28-19)16(9)24/h6-7,10-15,17-20,25H,1-5H3/t10-,11+,12?,13?,14?,15?,17-,18?,19+,20+,23?/m1/s1

2: InChI=1/C20H26O3/c1-9(2)14-13-8-11(4)12-7-6-10(3)15-16(21)17(22)19(14,5)18(23)20(12,13)15/h10-14,21H,1,6-8H2,2-5H3/t10-,11-,12+,13-,14-,19+,20-/m0/s1

3: InChI=1/C20H28O3/c1-10(2)8-14-9-12(4)15-7-6-11(3)16-18(22)17(21)13(5)19(23)20(14,15)16/h8,11-12,14-16,21H,6-7,9H2,1-5H3/t11-,12-,14?,15+,16-,20-/m1/s1

4: InChI=1/C19H22O5/c1-10-11-4-7-18(13(10)21)17-9-23-15(22)19(18,8-11)24-14(17)16(2,3)6-5-12(17)20/h5-6,10-11,14H,4,7-9H2,1-3H3/t10-,11-,14-,17?,18-,19+/m1/s1

5: InChI=1/C23H28O7/c1-8(2)6-11-23-10(22(3,4)27-5)7-9-12(15(25)18-17(29-18)14(9)24)13(23)16(28-11)19-20(30-19)21(23)26/h6-7,10-13,15-20,25H,1-5H3/t10-,11+,12?,13?,15+,16+,17-,18-,19-,20?,23-/m0/s1

Castro and Karney¹ previously predicted a Möbius aromatic transition state for the π-bond shift in [12]annulene (see Chapter 2.4.3.1), a process they termed “twist-couple bond shifting”. In late 2006 they turned their attention to the conformational surface of [16]annulene, searching again for Möbius aromatic ground or transition states.²

Oth synthesized [16]annulene by the photolysis of cycloctatetraene dimer. He observed two isomers 1a and 2a in a 83:17 ratio³ at -140 °C, with a barrier⁴ of 10.3 kcal mol^-1 separating them. The ¹H NMR spectrum at -30 °C shows only one signal. The equivalence of all of the protons implicates rapid conformational changes and bond shifting, as suggested in Scheme 1. Also noted was that these conversions, including the configuration change from 1 to 2, have barriers much lower than for the electrocyclization of Reaction 1 of about 22 kcal mol^-1.⁵

Scheme 1
	Reaction 1

Following on the results from their [12]annulene study, Castro and Karney optimized geometries at BH&HLYP/6-311+G(d,p). Since, as we discussed in Chapter 2.4.3.1, relative energies of annulene conformations are very sensitive to the computational method and basis set, they determined estimated CCSD(T)/cc-pVDZ energies, which I will call E_est, according to a prescription proposed by Bally and MacMahon,⁶ namely

The optimized structures of 1a and 2a are drawn in Figure 1. Both molecules are not planar, their bond lengths are clearly alternating, and their NICS(0) values are +6.4 ppm (1a) and +7.3 ppm (2a), all evidence that neither molecule is aromatic. 1a is predicted to be 0.8 kcal mol^-1 lower in energy than 2a, consistent with experiment.

1a (0.0) xyz file	1b (5.6) xyz file
1c (5.4) xyz file	1d (7.7) xyz file
2a (0.8) xyz file	2b (4.1) xyz file
TS-1c2b (13.7) xyz file

Figure 1. BH&HLYP/6-311+G(d,p) optimized geometries and relative energies (kcal mol^-1) based on E_est.²

The conformational change 1a → 1a’ is a multi-step process. This is in contrast to [12]annulene where this change occurs via a concerted mechanism. So, 1a first converts to 1c through a barrier of 7.9 kcal mol^-1. The path now splits; 1b can next be formed with a barrier of 9.4 kcal mol^-1 to give 1c’ or 1d can be formed through a barrier of 7.7 kcal mol^-1 to produce 1c’. 1c’ converts to 1a’ with a barrier of 7.9 kcal mol^-1. The structures of the intermediates and their relative energies are shown in Figure 1.

The conversion of 1 to 2 takes place through the transition state TS-1c2b that actually connects isomer 1c to 2b. This structure, shown in Figure 1, exhibits little bond alternation and has a NICS(0) value of -14.2, both strongly suggestive of Möbius aromatic character. Aromaticity should also imply energetic stabilization; TS-1c2b lies only 13.7 kcal mol^-1 above 1a. This barrier is less than that predicted for the twist-coupled bond shift in either [10]annulene or [12]annulene.

The highest barrier for the various interconversions indicated in Scheme 1 is the barrier associated with TS-1c2b. This barrier (13.7 kcal mol^-1) is significantly lower that the activation energy for Reaction 1 (22 kcal mol^-1). These computations confirm that the scrambling of the protons of [16]annulene is due to the rapid rearrangements of Scheme 1. Furthermore, the computations demonstrate that the key step is a twist-coupled bond shift that is facilitated by the Möbius aromatic character of its transition state.

Since the configuration change in [12]- and [16]annulene proceeds with a bond-shifting Möbius aromatic bond shifting transition state, might not the configuration change of [14]annulene proceed through a Möbius antiaromatic bond shifting transition state? In 2007, Castro and Karney⁷ answered this question in the affirmative.

Consistent with their previous studies, geometries were optimized at UBH&HLYP/6-311+G**. The unrestricted method is necessary since the expected antiaromatic transition state will have singlet radical character. In order to obtain reasonable energies, CASPT2(14,14)/cc-pVDZ single-point computations were employed.

[14]annulene must undergo two conformational changes (3a-c) before the bond shift/configuration change can occur through transition state 4 to give 5. Note that this process changes the number of cis and trans double bonds. This overall process is shown in Figure 2. The optimized structures of 3c, 4, and 5 are shown in Figure 3.

Figure 2. CASPT2(14,14)/cc-pVDZ// UBH&HLYP/6-311+G** relative energies of stable structures along the pathway for configuration change of [14]annulene.

The computed barrier for the configuration change (through 4) is computed to be 19.3 kcal mol-1, in very reasonable agreement with the experimental value⁴ of 21.3 kcal mol-1.

3c

4

5

Figure 3. UBH&HLYP/6-311+G** optimized geometries of 3c, 4, and 5.⁷

Based on its magnetic properties, transition state 4 has decided antiaromatic character. Its computed NICS(0) value is +19.0 ppm. Compare this to the NICS(0) values for 3a and 5 of -8.0 and -5.0 ppm, respectively. In addition, the computed chemical shifts of the two interior protons are very downfield, 26.4 and 26.7 ppm.

InChI

1: InChI=1/C16H16/c1-2-4-6-8-10-12-14-16-15-13-11-9-7-5-3-1/h1-16H/b2-1-,3-1-,4-2+,5-3+,6-4+,7-5+,8-6-,9-7-,10-8-,11-9-,12-10+,13-11+,14-12+,15-13+,16-14-,16-15-

2: InChI=1/C16H16/c1-2-4-6-8-10-12-14-16-15-13-11-9-7-5-3-1/h1-16H/b2-1-,3-1-,4-2+,5-3+,6-4+,7-5+,8-6-,9-7+,10-8+,11-9+,12-10+,13-11-,14-12-,15-13-,16-14+,16-15+

3: InChI=1/C14H14/c1-2-4-6-8-10-12-14-13-11-9-7-5-3-1/h1-14H/b2-1-,3-1-,4-2+,5-3+,6-4+,7-5+,8-6-,9-7-,10-8+,11-9+,12-10+,13-11+,14-12-,14-13-

5: InChI=1/C14H14/c1-2-4-6-8-10-12-14-13-11-9-7-5-3-1/h1-14H/b2-1-,3-1-,4-2-,5-3+,6-4+,7-5+,8-6+,9-7-,10-8-,11-9-,12-10-,13-11-,14-12+,14-13+

References

(1) Castro, C.; Karney, W. L.; Valencia, M. A.; Vu, C. M. H.; Pemberton, R. P., “Möbius Aromaticity in [12]Annulene: Cis-Trans Isomerization via Twist-Coupled Bond Shifting,” J. Am. Chem. Soc. 2005, 127, 9704-9705, DOI: 10.1021/ja052447j.

(2) Pemberton, R. P.; McShane, C. M.; Castro, C.; Karney, W. L., “Dynamic Processes in [16]Annulene: Change,” J. Am. Chem. Soc. 2006, 128, 16692-16700, DOI: 10.1021/ja066152x

(3) Oth, J. F. M.; Anthoine, G.; Gilles, J.-M., “Le dianion du [16] annulene,” Tetrahedron Lett. 1968, 9, 6265-6270, DOI: 10.1016/S0040-4039(00)75449-9.

(4) Oth, J. F. M., “Conformational Mobility and Fast Bond Shift in the Annulenes,” Pure Appl. Chem. 1971, 25, 573-622.

(5) Schroeder, G.; Martin, W.; Oth, J. F. M., “Thermal and Photochemical Behavior of a [16]Annulene,” Angew. Chem. Int. Ed. Engl. 1967, 6, 870-871, DOI: 10.1002/anie.196708701.

(6) Matzinger, S.; Bally, T.; Patterson, E. V.; McMahon, R. J., “The C₇H₆ Potential Energy Surface Revisited: Relative Energies and IR Assignment,” J. Am. Chem. Soc. 1996, 118, 1535-1542, DOI: 10.1021/ja953579n.

(7) Moll, J. F.; Pemberton, R. P.; Gutierrez, M. G.; Castro, C.; Karney, W. L., “Configuration Change in [14]Annulene Requires Möbius Antiaromatic Bond Shifting,” J. Am. Chem. Soc. 2007, 129, 274-275, DOI: 10.1021/ja0678469.

We noted in Chapter 2.1 some serious errors in the prediction of bond dissociation energies using B3LYP. For example, Gilbert examined the C-C bond dissociation energy of some simple branched alkanes.¹ The mean absolute deviation (MAD) for the bond dissociation energy predicted by G3MP2 is 1.7 kcal mol^-1 and 2.8 kcal mol^-1 using MP2. In contrast, the MAD for the B3LYP predicted values is 13.7 kcal mol^-1, with some predictions in error by more than 20 kcal mol^-1. Furthermore, the size of the error increases with the size of the molecule. Consistent with this trend, Curtiss and co-workers noted a systematic underestimation of the heat of formation of linear alkanes of nearly 0.7 kcal mol^-1 per bond using B3LYP.²

Further evidence disparaging the general performance of DFT methods (and B3LYP in particular) was presented in a paper by Grimme and in two back-to-back Organic Letters articles, one by Schreiner and one by Schleyer. Grimme³ noted that the relative Energy of two C₈H₁₈ isomers, octane and 2,2,3,3-tetramethylbutane are incorrectly predicted by DFT methods (Table 1). While MP2 and CSC-MP2 (spin-component-scaled MP2) correctly predict that the more branched isomer is more stable, the DFT methods predict the inverse! Grimme attributes this error to a failure of these DFT methods to adequately describe medium-range electron correlation.

Schreiner⁵ also compared the energies of hydrocarbon isomers. For example, the three lowest energy isomers of C₁₂H₁₂ are 1-3, whose B3LYP/6-31G(d) structures are shown in Figure 1. What is disturbing is that the relative energies of these three isomers depends strongly upon the computational method (Table 2), especially since these three compounds appear to be quite ordinary hydrocarbons. CCSD(T) predicts that 2 is about 15 kcal mol^-1 less stable than 1 and that 3 lies another 10 kcal mol^-1 higher in energy. MP2 exaggerates the separation by a few kcal mol^-1. HF predicts that 1 and 2 are degenerate. The large HF component within B3LYP leads to this DFT method’s poor performance. B3PW91 does reasonably well in reproducing the CCSD(T) results.

1 xyz file

2 xyz file

3 xyz file

Figure 1. Structures of 1-3 at B3LYP/6-31G(d).

Another of Schreiner’s examples is the relative energies of the C₁₀H­₁₀ isomers; Table 3 compares their relative experimental heats of formation with their computed energies. MP2 adequately reproduces the isomeric energy differences. B3LYP fairs quite poorly in this task. The errors seem to be most egregious for compounds with many single bonds. Schreiner recommends that while DFT-optimized geometries are reasonable, their energies are unreliable and some non-DFT method should be utilized instead.

Schleyer’s example of poor DFT performance is in the isodesmic energy of Reaction 1 evaluated for the n-alkanes.⁶ The energy of this reaction becomes more positive with increasing chain length, which Schleyer attributes to stabilizing 1,3-interactions between methyl or methylene groups. (Schleyer ascribes the term “protobranching” to this phenomenon.) The stabilization energy of protobranching using experimental heats of formation increases essentially linearly with the length of the chain, as seen in Figure 2.

n-CH₃(CH₂)_mCH₃ + mCH₄ → (m + 1)C₂H₆         Reaction 1

Schleyer evaluated the protobranching energy using a variety of methods, and these energies are also plotted in Figure 2. As expected, the G3 predictions match the experimental values quite closely. However, all of the DFT methods underestimate the stabilization energy. Most concerning is the poor performance of B3LYP. All three of these papers clearly raise concerns over the continued widespread use of B3LYP as the de facto DFT method. Even the new hybrid meta-GGA functionals fail to adequately predict the protobranching phenomenon, leading Schleyer to conclude: “We hope that Check and Gilbert’s pessimistic admonition that ‘a computational chemist cannot trust a one-type DFT calculation’¹ can be overcome eventually”. These papers provide a clear challenge to developers of new functionals.

Figure 2. Comparison of computed and experimental protobranching stabilization energy (as defined in Reaction 1) vs. m, the number of methylene groups of the n-alkane chain.⁶

Truhlar believes that one of his newly developed functionals answers the call for a reliable method. In a recent article,⁴ Truhlar demonstrates that the M05-2X⁷ functional performs very well in all three of the cases discussed here. In the case of the C₈H₁₈ isomers (Table 1), M05-2X properly predicts that 2,2,3,3-tetramethylbutane is more stable than octane, and estimates their energy difference within the error limit of the experiment. Second, M05-2X predicts the relative energies of the C₁₂H₁₂ isomers 1-3 within a couple of kcal mol^-1 of the CCSD(T) results (see Table 2). Last, in evaluating the isodesmic energy of Reaction 1 for hexane and octane, M05-2X/6-311+G(2df,2p) predicts energies of 11.5 and 17.2 kcal mol^-1 respectively. These are in excellent agreement with the experimental values of 13.1 kcal mol^-1 for butane and 19.8 kcal mol^-1 for octane.

Truhlar has also touted the M05-2X functional’s performance in handling noncovalent interactions.⁸ For example, the mean unsigned error (MUE) in the prediction of the binding energies of six hydrogen-bonded dimers is 0.20 kcal mol^-1. This error is comparable to that from G3 and much better than CCSD(T). With the M05-2X functional already implemented within NWChem and soon to be released within Gaussian and Jaguar, it is likely that M05-2X may supplant B3LYP as the new de facto functional in standard computational chemical practice.

Schleyer has now examined the bond separation energies of 72 simple organic molecules computed using a variety of functionals,⁹ including the workhorse B3LYP and Truhlar’s new M05-2X. Bond separation energies are defined by reactions of each compound, such as three shown below:

The new M05-2X functional performed the best, with a mean absolute deviation (MAD) from the experimental energy of only 2.13 kcal mol^-1. B3LYP performed much worse, with a MAD of 3.96 kcal mol^-1. As noted before, B3LYP energies become worse with increasing size of the molecules, but this problem is not observed for the other functionals examined (including PW91, PBE, and mPW1PW91, among others). So while M05-2X overall appears to solve many of the problems noted with common functionals, it too has some notable failures. In particular, the error is the bond separation energies of 4, 5, and 6 is -8.8, -6.8, and -6.0 kcal mol^-1, respectively.

References

(1) Check, C. E.; Gilbert, T. M., “Progressive Systematic Underestimation of Reaction Energies by the B3LYP Model as the Number of C-C Bonds Increases: Why Organic Chemists Should Use Multiple DFT Models for Calculations Involving Polycarbon Hydrocarbons,” J. Org. Chem. 2005, 70, 9828-9834, DOI: 10.1021/jo051545k.

(2) Redfern, P. C.; Zapol, P.; Curtiss, L. A.; Raghavachari, K., “Assessment of Gaussian-3 and Density Functional Theories for Enthalpies of Formation of C₁-C₁₆ Alkanes,” J. Phys. Chem. A 2000, 104, 5850-5854, DOI: 10.1021/jp994429s.

(3) Grimme, S., “Seemingly Simple Stereoelectronic Effects in Alkane Isomers and the Implications for Kohn-Sham Density Functional Theory,” Angew. Chem. Int. Ed. 2006, 45, 4460-4464, DOI: 10.1002/anie.200600448

(4) Zhao, Y.; Truhlar, D. G., “A Density Functional That Accounts for Medium-Range Correlation Energies in Organic Chemistry,” Org. Lett. 2006, 8, 5753-5755, DOI: 10.1021/ol062318n

(5) Schreiner, P. R.; Fokin, A. A.; Pascal, R. A.; deMeijere, A., “Many Density Functional Theory Approaches Fail To Give Reliable Large Hydrocarbon Isomer Energy Differences,” Org. Lett. 2006, 8, 3635-3638, DOI: 10.1021/ol0610486

(6) Wodrich, M. D.; Corminboeuf, C.; Schleyer, P. v. R., “Systematic Errors in Computed Alkane Energies Using B3LYP and Other Popular DFT Functionals,” Org. Lett. 2006, 8, 3631-3634, DOI: 10.1021/ol061016i

(7) Zhao, Y.; Schultz, N. E.; Truhlar, D. G., “Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions,” J. Chem. Theory Comput. 2006, 2, 364-382, DOI: 10.1021/ct0502763.

(8) Zhao, Y.; Truhlar, D. G., “Assessment of Model Chemistries for Noncovalent Interactions,” J. Chem. Theory Comput. 2006, 2, 1009-1018, DOI: 10.1021/ct060044j.

(9) Wodrich, M. D.; Corminboeuf, C.; Schreiner, P. R.; Fokin, A. A.; Schleyer, P. v. R., “How Accurate Are DFT Treatments of Organic Energies?,” Org. Lett., 2007, 9, 1851-1854, DOI: 10.1021/ol070354w.

InChI

1: InChI=1/C11H10/c1-2-5-7-3(1)4(1)8-6(2)10-9(5)11(7,8)10/h1-10H

2: InChI=1/C12H12/c1-2-4-10-6-8-11-7-5-9(3-1)12(10)11/h1-12H

3: InChI=1/C12H12/c1-2-4-8-11(7-3-1)12-9-5-6-10-12/h1-12H

4: InChI=1/C6H6/c1-4-5(2)6(4)3/h1-3H2

5: InChI=1/C8H10/c1-3-7-5-6-8(7)4-2/h3-4H,1-2,5-6H2

6: InChI=1/C10H10/c1-2-8-5-6-9-4-3-7(1)10(8)9/h1-10H

In Chapter 2.2, we suggest that the experimental deprotonation energy (DPE) of cyclohexane is in doubt. G2MP2 predicts the DPE of cyclohexane is 414.5 kcal mol^-1, a figure significantly higher than the experimental¹ value of 404 kcal mol^-1. Given that the deviation between the G2MP2 computed DPE and experiment is about 2 kcal mol^-1, we suggest that cyclohexane should be re-examined.

In a recent JACS article,² Kass calls into question the experimental bond dissociation energies (BDE) of the small cycloalkanes. With his experimental determination of the BDE of both the vinyl and allylic positions of cyclobutene, Kass can compare experimental and computed BDEs for a range of hydrocarbon environments, as listed in Table 1. The two composite methods G3 and W1 provide excellent BDE values for the small alkanes, one acyclic alkene, and the small cyclic alkenes. These composite methods appear to accurately predict BDEs of hydrocarbons.

However, the small cyclic alkanes are dramatic outliers. The well-accepted experimental BDEs of cyclopropane, cyclobutane, and cyclohexane are 3-5 kcal mol^-1 lower than those predicted by the composite methods. Given the strong performance of the computational methods, and the difficulties associated with experimental determinations of BDEs, Kass suggests that the BDEs of these cycloalkanes are in error. Further experiments are deserved.

References

(1) NIST webbook, 2005, http://webbook.nist.gov/.

(2) Tian, Z.; Fattahi, A.; Lis, L.; Kass, S. R., "Cycloalkane and Cycloalkene C-H Bond Dissociation Energies," J. Am. Chem. Soc. 2006, 128, 17087-17092, DOI: 10.1021/ja065348u

(3) Yao, Y.-R. Handbook of Bond Dissociation Energies in Organic Compounds; CRC Press: Boca Raton, FL, 2003.

(4) CRC Handbook of Chemistry and Physics; 85th ed.; Lide, D. R., Ed.; CRC Press: Boca Raton, FL, 2004.

(5) Tsang, W. In Energetics of Stable Molecules and Reactive Intermediates, NATO Science Series C; Minas da Piedade, M. E., Ed.; Kluwer Academic Publishers: Dordrecht, Netherlands, 1999; Vol. 535.

(6) Fattahi, A.; McCarthy, R. E.; Ahmad, M. R.; Kass, S. R., "Why Does Cyclopropene Have the Acidity of an Acetylene but the Bond Energy of Methane?," J. Am. Chem. Soc. 2003, 125, 11746-11750, DOI: 10.1021/ja035725s.

(7) DeFrees, D. J.; McIver, R. T., Jr.; Hehre, W. J., "Heats of Formation of Gaseous Free Radicals via Ion Cyclotron Double Resonance Spectroscopy," J. Am. Chem. Soc. 1980, 102, 3334-3338, DOI: 10.1021/ja00530a005.

(8) Furuyama, S.; Golden, D. M.; Benson, S. W., "Kinetic Study of the Gas-Phase Reaction c-C₅H₈+I₂ c-C₅H₆+2HI. Heat of Formation and the Stabilization Energy of the Cyclopentenyl Radical," Int. J. Chem. Kinet. 1970, 2, 93-99.

(9) Alfassi, Z. B.; Feldman, L., "The Kinetics of Radiation-Induced Hydrogen Abstraction
by Trichloromethyl Radicals in the Liquid Phase: Cyclohexene," Int. J. Chem. Kinet. 1981, 13, 771-783.

Addition of enolboranes to α-substituted aldehydes

In Chapter 5.2, we discussed a number of computation studies of the origins of asymmetry in 1,2-additions. We discussed the importance of the Felkin-Anh model, but that modifications of this model are needed to rationalize the broad range of addition reactions.

One modification was presented by Frenking,¹ who noted that in the addition of LiH to propanal, it was the conformation of the aldehyde that dictated the energy of the possible transition states. The lowest energy transition state is 1a, lying 1.3 kcal mol^-1 below 1b and 1.6 kcal mol^-1 below 1c (computed at MP2/6-31G(d)//HF/6-31G(d)). When the LiH fragment is removed and all other atoms kept frozen in their positions in the three transition states, 1a remains the lowest in energy.

A recent article by Cramer and Evans² examined the addition of enolboranes to aldehydes and also noted the importance of the aldehyde conformation in dictating the stereochemical outcome. The main thrust was, however, that the Cram-Conforth type model for 1,2-addition is more appropriate for some enolborane additions.

This work derives from Evans’ earlier experimental study of the addition of the boron enolate of 2-methyl-3-pentanone to a-alkoxyaldehydes (Scheme 1).³ Evans suggested that there were four transition state models that give a 3,4-anti relationship in the product (Scheme 2). The Felkin-Anh model favors B, since it avoids the syn interaction, and so E enolates will have a greater anti selectivity than Z enolates. On the other hand, the Conforth model favors transition state C, and predicts that Z enolates will have greater anti selectivity. The addition of Z enolates in fact gives large anti selectivity, while addition of E enolates gives poor anti selectivity. These results are consistent with the Cram-Cornforth model.

Scheme 1.

Scheme 2.

Cee, Cramer and Evans² examined the addition of enolborane to a number of a-substituted propanal compounds. They located six transition states (Figure 1) for the reaction of 2-fluoropropanal, three leading to the (R,S) product (2A-C) and three leading to the (S,S) product (2A’-C’). The lowest energy transition states, 2A and 2A’, both have the fluorine atom positioned anti to the carbonyl, consistent with the Cornforth model. This reflects the stability of 2-fluoropropanal. Similar results are found for addition to 2-chloropropanal

2A (0.0) xyz file		2B (2.4) xyz file
2C (2.6) xyz file
2A’ (0.8) xyz file		2B’ (1.4) xyz file
2C’ (3.7) xyz file

Figure 1. Optimized transition states and relative energies (kcal mol^-1) for the reaction of 2-fluoropropanal with enolborane computed at B3LYP/6-31G(d).²

For the reaction of enolborane with 2-methoxypropanal, the lowest energy transition state, 3, also has the methoxy group anti to the carbonyl (see Figure 2). However, the lowest energy transition state for the reaction of 2-methylthiopropanal, 4, has the MeS group perpendicular to the carbonyl, as predicted by the Felkin-Anh model. Similarly, the lowest energy transition states for the addition to 2-dimethylaminopropanal (5) and to 2-dimenthylphosphinopropanal (6) follow the Felkin-Anh model.

The lowest energy conformer of propanal with F, Cl, or OMe as the 2-substituent has the substituent anti to the carbonyl. All three of these aldehydes undergo addition of enolborane through the Cornforth TS. The lowest energy conformer with SMe₂ or PMe₂ has the substituent perpendicular to the carbonyl, which mimics its location in the enolborane transition state. Only 2-dimethylaminopropanal falls outside this pattern; its lowest energy conformer positions the substituent about 150° from the carbonyl, but rotation to a perpendiculat (Felkin-Anh) position requires only 2 kcal mol^-1, half of that need for F, Cl, or methoxy rotation. Cee, Cramer, and Evans draw two conclusions. First, the stereochemistry 1,2-addition of enolborane parallels the conformation of the aldehyde itself, and second, this implies that the Cornforth pathway can be preferred over the Felkin-Anh for those aldehydes where the anti conformation is particularly stable.

3 xyz file		4 xyz file
5 xyz file		6 xyz file

References

(1) Frenking, G.; F., K. K.; Reetz, M. T., “On the Origin of π-Facial Diastereoselectivity in Nucleophilic Additions to Chiral Carbonyl Compounds. 2. Calculated Transition State Structures for the Addition of Nucleophiles to Propionaldehyde 1, Chloroacetyldehyde 2, and 2-Chloropropionaldehyde 3.,” Tetrahedron 1991, 47, 9005-9018, DOI: 10.1016/S0040-4020(01)86505-4.

(2) Cee, V. J.; Cramer, C. J.; Evans, D. A., “Theoretical Investigation of Enolborane Addition to α-Heteroatom-Substituted Aldehydes. Relevance of the Cornforth and Polar Felkin-Anh Models for Asymmetric Induction,” J. Am. Chem. Soc. 2006, 128, 2920-2930, DOI: DOI: 10.1021/ja0555670

(3) Evans, D. A.; Siska, S. J.; Cee, V. J., “Resurrecting the Cornforth Model for Carbonyl Addition: Studies on the Origin of 1,2-Asymmetric Induction in Enolate Additions to Heteroatom-Substituted Aldehydes,” Angew. Chem. Int. Ed. 2003, 42, 1761-1765, DOI: 10.1002/anie.200350979.

Monohydrated Glycolaldehyde (2-hydroxyethanal)

In Chapter 6.3.1 we discussed the conformation energy profile of solvated ethylene glycol and glycerol. The conformational preference is determined by the two competing hydrogen bonding interactions: intramolecular hydrogen bonding versus hydrogen bonding to the water molecules. For both glycerol and ethylene glycol, the lowest energy solvated structures retain the maximal number of internal hydrogen bonds possible.

The conformational space of glycoladehyde 1 exhibits four local minima. ¹ The lowest energy structure possesses an internal hydrogen bond, 1-CC (Figure 1). The other conformers are at least 3 kcal mol^-1 higher in energy. Will this internal hydrogen bond persist when 1 is hydrated?

1-CC (0.0) xyz file	1-TT (3.06) xyz file
1-TG (3.33) xyz file	1-CT (4.84) xyz file

Figure 1. Optimized geometries of the conformers of 1 at MP2/aug-cc-pVTZ. ¹ The letters C, T, and G indicate cis¸ trans, or gauche around the C-C and C-O bonds, in that order. Relative energies in kcal mol^-1.

A recent computational (B3LYP/6-311++G(2df,p)) and experimental study examined the structure of monohydrated glycoladehyde.² Optimization of the monohydrated cluster of 1 indicated that the lowest energy structures all have the glycolaldehyde fragment in the CC conformation (see Figure 2). The lowest energy cluster not in the CC arrangement is 1-TG-w, and it lies 2.86 kcal mol^-1 above the lowest monohydrate, 1-CC-w1.

The lowest energy monohydrate (1-CC-w1) does not maintain the internal hydrogen bond of 1-CC. Rather, the water molecule inserts into this hydrogen bond, such that it donates a hydrogen to the carbonyl oxygen, and accepts the hydrogen from the hydroxyl group. The other conformations provide no opportunity for forming two hydrogen bonds with a water molecule, and so their hydrates are higher in energy. The microwave FT spectrum² of the monohydrate of 1 is interpreted as a dynamic interconversion of the two lowest energy complexes, 1-CC-w1 and 1-CC-w2.

1-CC-w1 (0.0) xyz file	1-CC-w2 (0.51) xyz file
1-CC-w3 (0.96) xyz file	1-CC-w4 (1.39) xyz file
1-TG-w (2.86) xyz file	1-TT-w (3.71) xyz file
1-CT-w (5.98) xyz file

Figure 2. Optimized geometries (B3LYP/6-311++G(2df,p)) of the monohydrated glycolaldehyde structures.² All distances in Å and relative energies (G3MP2B3) in kcal mol^-1.

References

(1) Ratajczyk, T.; Pecul, M.; Sadlej, J.; Helgaker, T., “Potential Energy and Spin-Spin Coupling Constants Surface of Glycolaldehyde,” J. Phys. Chem. A 2004, 108, 2758-2769, DOI: 10.1021/jp0375315

(2) Aviles-Moreno, J. R.; Demaison, J.; Huet, T. R., “Conformational Flexibility in Hydrated Sugars: the Glycolaldehyde-Water Complex,” J. Am. Chem. Soc. 2006, 128, 10467-10473, DOI: 10.1021/ja062312t

A Stable Bis-allyl Intermediate on the Cope PES

As discussed in Chapter 3.2, the prototypical Cope rearrangement (the degenerate rearrangement of 1,5-hexadiene 1) is understood to proceed through a single concerted transition state. The concerted transition state 2 is described by three resonance structures (Scheme 1), and this allows for understanding the chameleonic nature of the substituted Cope rearrangement. For example, radical stabilizing groups at the 2 and 5 positions would favor the cyclohexyl-diyl structure.

Scheme 1

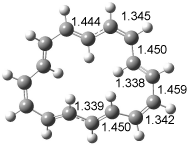
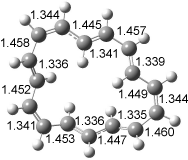
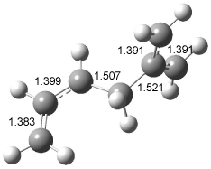
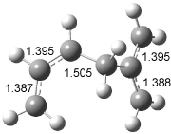
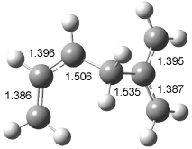
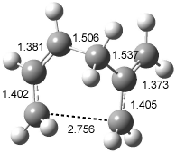
Schreiner computed the reaction path at BD(T)/cc-pVDZ//BLYP/6-31G* for 64 different variations of the Cope rearrangement.¹ A representative sampling from these is presented in Figure 1. The Cope rearrangements are found to fall into one of three categories. The first, called type 1, are concerted rearrangements. Type 2 rearrangements have two competing pathways: either through a concerted transition state or a diradical intermediate. The last group, type 3, comprises nonconcerted reactions with a cyclohexyl-diyl intermediate. Schreiner generalizes the results to the following rule: a nonconcerted reaction takes place when biradical intermediates are stabilized either by allyl or aromatic resonance.

Figure 1. Examples of the three type of Cope rearrangements. Relative energies, in kcal mol-1, were computed at BD(T)/cc-pVDZ//BLYP/6-31G*.1

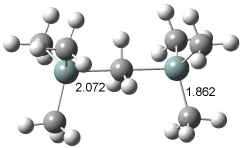
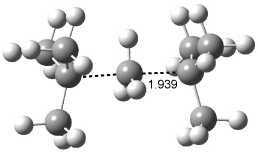
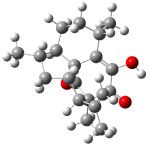
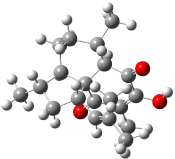
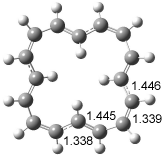
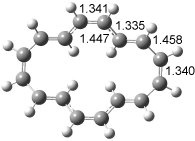
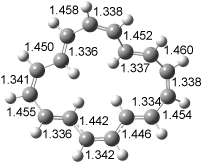
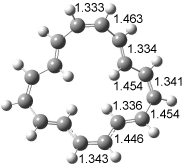
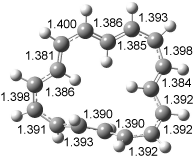
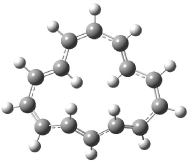
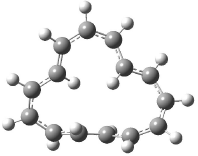
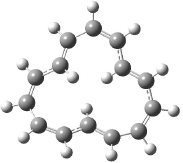
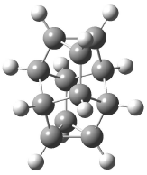
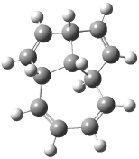
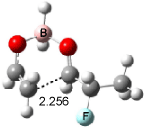
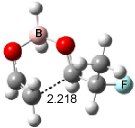
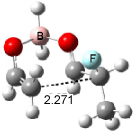
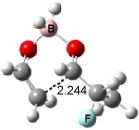
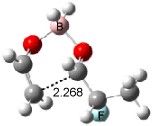
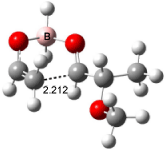
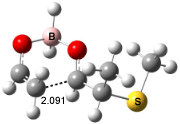
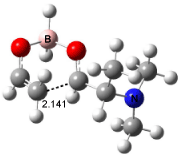
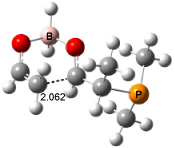
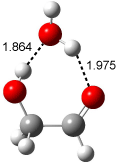
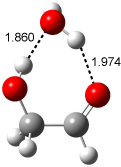
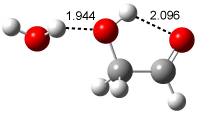
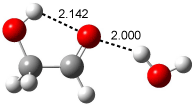
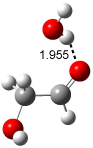
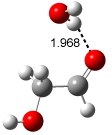
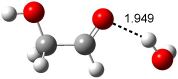
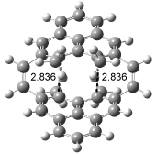
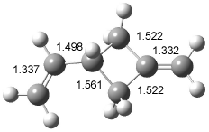
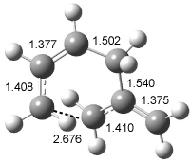
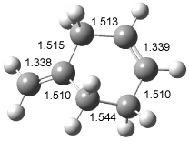
Interestingly, Schreiner’s study identified reactions where the diyl is a stable intermediate, but he identified no case where the other extreme – two allyl radicals – appeared as a stable intermediate. Kertesz, in 2006, discovered just such an example with the Cope rearrangement of 3.² Using B3LYP and BPW91 computations with two different basis sets, he identified the stable diradical 5. This structure, shown in Figure 2, clearly has very long distances – 2.836 Å – separating the ends of the two “allylic” components. A true transition state 4 connects the reactant 3 with the intermediate 5 (see Figure 2). The activation energy is 6.3 kcal mol^-1 and the intermediate 5 lies 3.3 kcal mol^-1 above 3.

3	4	5
xyz file	xyz file	xyz file
Figure 2. B3LYP/6-31G(d) optimized structures of 3-5. Distances (Å) shown are between C1-C6 and C3-C4 of the hexadiene component of the Cope rearrangement.2

Why does a stable bis-allyl analogue exist on the Cope reaction surface of 3? In the prototype Diels-Alder reaction of 1,5-hexadiene, the possible bis-allyl intermediate (i.e., two isolated allyl radicals) is about 26 kcal mol^-1 higher in energy than the Cope transition state. Only with significant radical stabilization might one expect a bis-allyl intermediate to occur. One can consider 5 as composed of two bridged phenalenyl radicals (6). Phenalenyl radical is stable due to electron delocalization; its ESR spectrum has been observed, but it has not been isolated, instead dimerizing to give 7.³ In addition to the stabilization afforded by the extensive delocalization of the radical within the phenalenyl system, two phenalenyl systems can also interact through overlap of their π-systems, creating what has been termed π-dimerization.^4-6 MRMP2 computations suggest that the π-dimerization energy of 6 is 11 kcal mol^-1.⁷ While the geometry of 5 is not ideal for π-dimerization, its structure clearly indicates some stacking of the two phenalenyl fragments. Both the enhanced electron delocalization about the large phenalenyl system along with π-dimerization provides sufficient stabilization that the bis-allyl intermediate exits on the Cope rearrangement pathway. This now completes all of the options for how the Cope rearrangement may occur: either directly through a concerted transition state, or multi-step process with a 1,6-diyl intermediate or a bis-allyl intermediate.

Cope Rearrangement of 3-Vinylmethylenecyclobutane

3-Vinylmethylenecyclobutane 8 can undergo a myriad of thermal rearrangements involving [1,3]- and [3,3]-shifts.⁸ The Cope rearrangement of 8 to 9 has a barrier of 35.7 kcal mol^-1.⁹ This large barrier is consistent with cleavage of a C-C bond leading to a diradical intermediate.

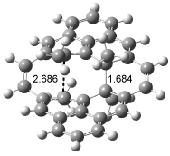
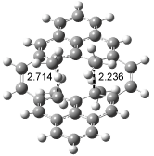
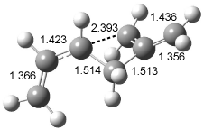
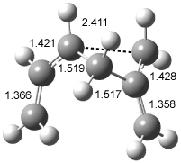
Houk has recently confirmed the diradical nature of this rearrangement.¹⁰ The geometries of all reactants intermediates, products and transition states were optimized at UB3LYP/6-31+G(d) and single-point energies were evaluated at CASPT2(6,6)/6-31G(d). Two diradical intermediates, 10 and 11, lie 30.0 and 32.0 kcal mol^-1, respectively, above 8. These intermediates are separated by a small barrier, 1.5 kcal mol^-1 from 10, and a barrier of 2.0 kcal mol^-1 interconverts mirror versions of 10. All of these paths are sketched in Scheme 3 and the geometries of the critical points are displayed in Figure 3.

Scheme 3

8 xyz file
TS8-10 xyz file	TS8-11 xyz file
10 xyz file	TS10-11 xyz file	11 xyz file
TS11-9x xyz file	TS11-9n xyz file
9 xyz file

Figure 3. Optimized Structures of the critical points in Scheme 3.¹⁰

Only the reaction going forward from 11 can lead to product 9. There are two such routes, involving an exo or endo approach. They are of similar energy, and also very close in energy to that of the diradical intermediates. Houk concludes that the diradical intermediates “have substantial conformational freedom and very low barriers for forming stereo- and regioisomeric forms of the ring-enlarged product”, in agreement with the experimentally observed lack of any region- or stereoselectivity in the thermal reactions of 8. The computed barrier, 34.9 kcal mol^-1 for TS8-10, is in good accord with the experimental barrier of 35.7 kcal mol^-1.

A study by Jung¹¹ the year before actually inspired Houk’s work. Jung discovered that appropriately substituted vinylmethylcyclohexenes will undergo very selective Cope rearrangements; for example, thermolysis of 8a produces 9a in greater than 90% yield. This result is quite contrary to that normally observed for vinylmethylcyclohexene thermoylsis: many products with virtually complete scrambling of all stereochemical information.

Examination of the rearrangement of 8a is computationally prohibitive, so Houk looked at the effect of individual substituents. The role of the trialkylsiloxy group was evaluated through the rearrangement of 8b, leading to diradicals 10b and 11b (Scheme 4). The transition state leading to 11b is 1.5 kcal mol^-1 below that leading to 10b. This is opposite the relative ordering of the transition states in the parent reaction, indicating that siloxy substitution would favor the path that leads to direct Cope rearrangement, which must pass through 11. The preference for the opposite TS with the siloxy group results from its torquoselectivity (See Chapter 3.5) Since 11b is more stable than 10b, this would also help preserve the stereochemistry during the rearrangement.

Scheme 4

The effects of the terminal substituents were also evaluated. As shown in Scheme 5, the Cope rearrangement of 8b is predicted to proceed with distinct stereoselectivity. The ring opening step preferentially produces diradical intermediate 12 over 13. The ring forming step is also stereoselective: 12 cyclizes to 14 in a 3:1 ratio, while the ring closure of 13 predominantly gives 15. Overall, the rearrangement of 8b is predicted to give a product ratio 14:15 of 2:1. This is in accord with the Jung’s experimental observation.

Scheme 5

References

(1) Navarro-Vazquez, A.; Prall, M.; Schreiner, P. R., “Cope Reaction Families: To Be or Not to Be a Biradical,” Org. Lett. 2004, 6, 2981-2984, DOI: 10.1021/ol0488340

(2) Huang, J.; Kertesz, M., “Stepwise Cope Rearrangement of Cyclo-biphenalenyl via an Unusual Multicenter Covalent π-Bonded Intermediate,” J. Am. Chem. Soc. 2006, 128, 7277-7286, DOI: 10.1021/ja060427r

(3) Zheng, S.; Lan, J.; Khan, S. I.; Rubin, Y., “Synthesis, Characterization, and Coordination Chemistry of the 2-Azaphenalenyl Radical,” J. Am. Chem. Soc. 2003, 125, 5786-5791, DOI: 10.1021/ja029236o

(4) Goto, K.; Kubo, T.; Yamamoto, K.; Nakasuji, K.; Sato, K.; Shiomi, D.; Takui, T.; Kubota, M.; Kobayashi, T.; Yakusi, K.; Ouyang, J., “A Stable Neutral Hydrocarbon Radical: Synthesis, Crystal Structure, and Physical Properties of 2,5,8-Tri-tert-butyl-phenalenyl,” J. Am. Chem. Soc. 1999, 121, 1619-1620, DOI: 10.1021/ja9836242

(5) Suzuki, S.; Morita, Y.; Fukui, K.; Sato, K.; Shiomi, D.; Takui, T.; Nakasuji, K., “Aromaticity on the Pancake-Bonded Dimer of Neutral Phenalenyl Radical as Studied by MS and NMR Spectroscopies and NICS Analysis,” J. Am. Chem. Soc. 2006, 128, 2530-2531, DOI: 10.1021/ja058387z

(6) Takano, Y.; Taniguchi, T.; Isobe, H.; Kubo, T.; Morita, Y.; Yamamoto, K.; Nakasuji, K.; Takui, T.; Yamaguchi, K., “Hybrid Density Functional Theory Studies on the Magnetic Interactions and the Weak Covalent Bonding for the Phenalenyl Radical Dimeric Pair,” J. Am. Chem. Soc. 2002, 124, 11122-11130, DOI: 10.1021/ja0177197

(7) Small, D.; Zaitsev, V.; Jung, Y.; Rosokha, S. V.; Head-Gordon, M.; Kochi, J. K., “Intermolecular π-to-π Bonding between Stacked Aromatic Dyads. Experimental and Theoretical Binding Energies and Near-IR Optical Transitions for Phenalenyl Radical/Radical versus Radical/Cation Dimerizations,” J. Am. Chem. Soc. 2004, 126, 13850-13858, DOI: 10.1021/ja046770i

(8) Kozhushkov, S. I.; Kuznetsova, T. S.; Zefirov, N. S., “Mechanism of Thermal Isomerization of 3-Vinylmethylenecyclobutane into 4-Methylenecyclohexane,” Dokl. Akad. Nauk SSSR, 1988, 299, 1395-1399,

(9) Dolbier, W. R.; Mancini, G. J., “Non-concerted Thermal Reorganizations 3,3-Divinylmethylenecyclobutane,” Tetrahedron Lett. 1975, 16, 2141-2144, DOI: 10.1016/S0040-4039(00)72661-X.

(10) Zhao, Y. L.; Suhrada, C. P.; Jung, M. E.; Houk, K. N., “Theoretical Investigation of the Stereoselective Stepwise Cope Rearrangement of a 3-Vinylmethylenecyclobutane,” J. Am. Chem. Soc. 2006, 128, 11106-11113, DOI: 10.1021/ja060913e

(11) Jung, M. E.; Nishimura, N.; Novack, A. R., “Versatile Diastereoselectivity in Formal [3,3]-Sigmatropic Shifts of Substituted 1-Alkenyl-3-alkylidenecyclobutanols and Their Silyl Ethers,” J. Am. Chem. Soc. 2005, 127, 11206-11207, DOI: 10.1021/ja051663p

InChI

3: InChI=1/C34H26/c1-19-21-11-12-22-16-24-8-6-10-26-18-28-14-13-27-17-25-9-5-7-23(15-21)29(25)31(19)33(27,3)34(28,4)32(20(22)2)30(24)26/h5-18H,1-4H3/b12-11-/t33-,34+

5: InChI=1/C34H26/c1-19-23-11-12-25-17-29-9-6-10-30-18-26(22(4)32(21(25)3)34(29)30)14-13-24-16-28-8-5-7-27(15-23)33(28)31(19)20(24)2/h5-18H,1-4H3/b12-11-,14-13-

6: InChI=1/C13H9/c1-4-10-6-2-8-12-9-3-7-11(5-1)13(10)12/h1-9H

7: InChI=1/C26H18/c1-5-17-9-3-11-23-21(15-13-19(7-1)25(17)23)22-16-14-20-8-2-6-18-10-4-12-24(22)26(18)20/h1-16,21-22H

8: InChI=1/C7H10/c1-3-7-4-6(2)5-7/h3,7H,1-2,4-5H2

9: InChI=1/C7H10/c1-7-5-3-2-4-6-7/h2-3H,1,4-6H2

Today I launch this blog – a blog to accompany my new book Computational Organic Chemistry. The book is officially released today – so go out and buy a copy before you get all tied up with the new Harry Potter!

This blog serves mainly to update the book. I will post on new articles and web sites that relate to topics covered in the book. It also serves as a mechanism to get feedback from you the reader. I welcome all comments, corrections, and suggestions.

I will also try to utilize new technologies within the post. Structures of molecules are available as xyz-coordinates and also directly within the blog using the JMol utility. I have added InChIs for most compounds. Articles are referenced by DOIs. Other technologies, like RDFa will be introduced in the future.

Enjoy!