Bertran and Wipf have examined the role of solvent organization about a chiral molecule in producing the optical activity.¹ They generated 1000 configurations of benzene arrayed about methyloxirane from a Monte Carlo simulation. Each configuration was then constructed by keeping every benzene molecules within 0.5 nm from the center-of-mass of methyloxirane, usually 8-10 solvent molecules. The optical rotation was then computed at four wavelengths using TDDFT at BP86/SVP. (The authors note that though the Gaussian group recommends B3LYP/aug-ccpVDZ,^2-4 using the non-hybrid functional allows the use of resolution-of–the-identity⁵ techniques that make the computations about six orders of magnitude faster – of critical importance given the size of the clusters and the sheer number of them!) Optical rotation is then obtained by averaging over the ensemble.

The computed optical rotations disagree with the experiment by about 50% in magnitude but have the correct sign across the four different wavelengths. Use of the COSMO model (implicit solvent) provides the wrong sign at short wavelengths. But perhaps most interesting is that the computed optical activity of the solvent molecules in the configuration about the solute, but without including methyloxirane, is nearly identical to that of the whole cluster! In other words, the optical activity is due to the dissymmetric distribution of the solvent molecules about the chiral molecule, not the chiral molecule itself! It is the imprint of the chiral molecule on the solvent ordering that accounts for nearly all of the optical activity.

References

(1) Mukhopadhyay, P.; Zuber, G.; Wipf, P.; Beratan, D. N., "Contribution of a Solute’s
Chiral Solvent Imprint to Optical Rotation," Angew. Chem. Int. Ed. 2007,
46, 6450-6452, DOI: 10.1002/anie.200702273

(2) Stephens, P. J.; McCann, D. M.; Cheeseman, J. R.; Frisch, M. J., "Determination of
absolute configurations of chiral molecules using ab initio time-dependent Density Functional Theory calculations of optical rotation: How reliable are absolute configurations obtained for molecules with small rotations?," Chirality 2005, 17, S52-S64, DOI: 10.1002/chir.20109.

(3) Stephens, P. J.; Devlin, F. J.; Cheeseman, J. R.; Frisch, M. J., "Calculation of Optical Rotation Using Density Functional Theory," J. Phys. Chem. A 2001, 105, 5356-5371, DOI: 10.1021/jp0105138.

(4) Stephens, P. J.; McCann, D. M.; Devlin, F. J.; Flood, T. C.; Butkus, E.; Stoncius,
S.; Cheeseman, J. R., "Determination of Molecular Structure Using Vibrational Circular Dichroism Spectroscopy: The Keto-lactone Product of Baeyer-Villiger Oxidation of (+)-(1R,5S)-Bicyclo[3.3.1]nonane-2,7-dione," J. Org. Chem. 2005, 70, 3903-3913, DOI: 10.1021/jo047906y.

(5) Eichkorn, K.; Treutler, O.; Ohm, H.; Haser, M.; Ahlrichs, R., "Auxiliary Basis Sets to Approximate Coulomb Potentials," Chem. Phys. Lett. 1995, 240, 283-289, DOI: 10.1016/0009-2614(95)00621-A.

In 2001, Pophristic and Goodman¹ initiated a controversy over the nature of the rotational barrier in ethane. Most organic textbooks argue that the barrier is due to unfavorable steric interactions in the eclipsed conformation. The Nature paper argues rather that the staggered conformation is favored due to hyperconjugative interactions between the C-H bond orbital on one methyl interacting with the anti-disposed antibonding C-H orbital of the other methyl group. Schreiner² wrote a follow-up essay where he was surprised by the response to this paper since he thought that the hyperconjugative explanation had been well-accepted within the community.

Now we have a nice review article by Mo and Gao³ that summarizes their recent investigation of the rotational barrier of ethane. Their main approach is to take advantage of the block localization method. Essentially, the methyl e-orbitals are localized to each methyl group, forbidding any hyperconjugation with each other. The energy difference then between the fully relaxed ethane and the block localized energy accounts for hyperconjugation – and this is about 0.76 kcal/mol, or about 25% of the barrier. The most important contributing factor to the barrier is the steric component – this is estimated by comparing the energies of the staggered and eclipsed conformers while freezing the π-like orbitals and removing the hyperconjugation effects. The estimate for the steric component is 2.73 kcal/mol. Mo and Gao conclude that the simple, traditional explanation, namely that steric interactions destabilize the eclipsed conformation, is in fact correct.

References

(1) Pophristic, V.; Goodman, L., "Hyperconjugation not Steric Repulsion leads to the Staggered Structure of Ethane," Nature 2001, 411, 565-568, DOI: 10.1038/35079036.

(2) Schreiner, P. R., "Teaching the Right Reasons: Lessons from the Mistaken Origin of the Rotational Barrier in Ethane," Angew. Chem. Int. Ed. 2002, 41, 3579-3582, DOI: 10.1002/1521-3773(20021004)41:19<3579::AID-ANIE3579>3.0.CO;2-S

(3) Mo, Y.; Gao, J., "Theoretical Analysis of the Rotational Barrier of Ethane," Acc. Chem. Res., 2007, 40, 113-119, DOI: 10.1021/ar068073w

A growing area for the application of computational chemistry is in the structural identification of compounds. In the book, I discussed the use of computed IR spectra to identify intermediates in the photolysis of phenyl nitrene and carbine and the benzynes. In previous blogs, I have written posts (here, here and here) about recent use of computed NMR spectra to discern the structure of new natural products. With this post I discus the use of computed optical activity to determine the absolute configuration of molecules.

Rosini and co-workers have examined a number of oxygenated cyclohexene epoxides.to explore the use of TDDFT computed optical activity as a means for determining absolute configuration.¹ In chapter 1.6.3, I discuss the work of the Gaussian team on benchmarking optical rotation and ORD. They find that B3LYP/aug-cc-pVDZ computed optical activities are in quite reasonable agreement with experiment.^2-4 In this work, Rosini explores using a smaller basis set (6-31G(d)), the role of solvent, and also if computed spectra can be used to assess the absolute configuration of new molecules.

They first benchmark the B3LYP/6-31G(d) computed optical activities for a number of related cyclohexene epoxides against B3LYP/aug-cc-pVDZ and experimental values. I will begin by discussing two of their examples: (+)-chaloxone 1 (PubChem)
and (+)-epoxydon 2
(PubChem).

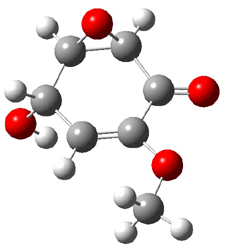
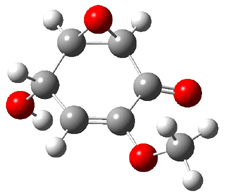
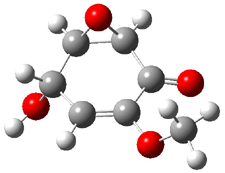
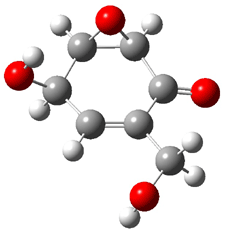
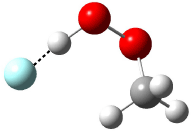
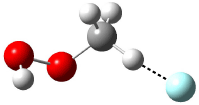
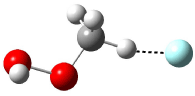
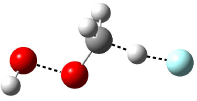
Five conformations of 1 were optimized in the gas phase and then their optical activities for the sodium D line were computed using TDDFT with both the small and larger basis set. These computations were then repeated to model the effect of solvent using PCM; the solution (methanol) B3LYP/6-31G(d) structures are shown in Figure 1.

1a 0.0	1b 2.40	1c 0.87
1d 1.02	1e 3.12

Figure 1. PCM(methanol)/B3LYP/6-31G(d) optimized structures of 1. Relative free energies of each conformer in kcal/mol.¹

The optical rotation at the sodium D line was then computed with TDDFT in both gas and solution phase with the smaller and larger basis set. The values were then averaged base on a Boltzmann weighting using the computed free energies of each conformer. The optical rotation for each conformer and the average values are listed in Table 1. The experimental optical rotation is +271. The authors note that while the gas phase B3LYP/6-31G(d) average value is far off the experimental value, it does predict the correct sign, and since all of the five conformers give rise to a positive rotation, any error in the energies will not affect the sign. The computed gas phase value with the larger basis set is in better agreement with experiment. However, it is still too large, but the solution values are much better. In fact, the PCM/B3LYP/aug-cc-pVDZ value is in excellent agreement with experiment.

Table 1. Computed optical activity of the conformers of 1 in gas and solution phase.

^aBased on a Boltzmann weighting of the population of each conformation.

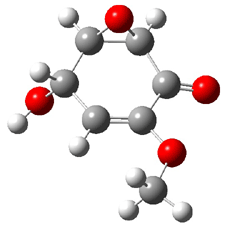
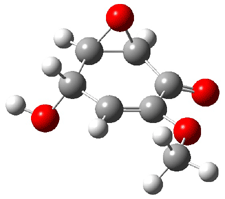
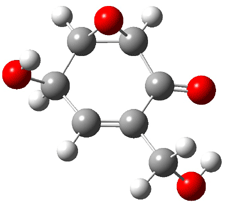
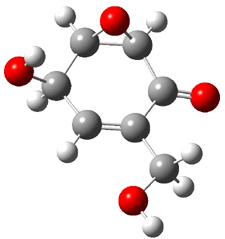
Five conformers of epoxydon 2 were also located, and the computed solution structures are shown in Figure 2. The computed optical rotations for both the gas and solution phase for these structures (and the Boltzmann weighted averages) are listed in Table 2. The experimental value for the optical rotation of 2 is +93.

2a 0.0	2b 0.32	2c 0.23
2d 0.22	2e 0.66

Figure 2. PCM(methanol)/B3LYP/6-31G(d) optimized structures of 2. Relative free energies of each conformer in kcal/mol.¹

In this case, the small basis set performs very poorly. The gas phase B3LYP/6-31G(d) value
of [α]_D is -16, predicting the wrong sign, let alone the wrong magnitude. Things improve with the larger basis set, which predicts a value of +57. Since conformer 2ais levorotatory and the other four are dextrorotatory, the computed relative energies are key to getting the correct prediction. This is made even more poignant with the solution results, where the PCM/B3LYP/aug-cc-pVDZ prediction is quite acceptable.

Table 2. Computed optical activity of the conformers of 2 in gas and solution phase.

^aBased on a Boltzmann weighting of the population of each conformation.

Threy conclude with two examples of application of computation to assignment of structure. I discuss here the absolute configuration of (-)-sphaeropsidone 3 (PubChem).
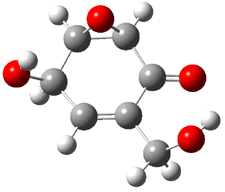
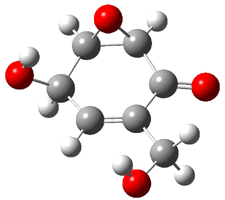
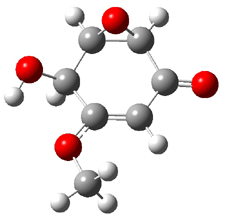
Rosini located two conformations of 3, shown in Figure 3. The computed optical rotations are listed in Table 3. The experimental value for 3 is -130. Both conformers are computed to be dextrorotatory with all computational methods. The magnitude of the computed values using the larger basis set is in nice agreement with experiment, but the sign is wrong. Rosini concludes that the absolute configuration of 3 has been misassigned.

3a 0.06

3b 0.0

Figure 3. PCM(methanol)/B3LYP/6-31G(d) optimized structures of 3. Relative free energies of each conformer in kcal/mol.¹

Table 3. Computed optical activity of the conformers of 3 in gas and solution phase.

^aBased on a Boltzmann weighting of the population of each conformation.

References

(1) Mennucci, B.; Claps, M.; Evidente, A.; Rosini, C., "Absolute Configuration of Natural Cyclohexene Oxides by Time Dependent Density Functional Theory Calculation of the Optical Rotation: The Absolute Configuration of (-)-Sphaeropsidone and (-)-Episphaeropsidone Revised," J. Org. Chem. 2007, 72, 6680-6691, DOI: 10.1021/jo070806i

(2) Stephens, P. J.; Devlin, F. J.; Cheeseman, J. R.; Frisch, M. J., "Calculation of Optical Rotation Using Density Functional Theory," J. Phys. Chem. A 2001, 105, 5356-5371, DOI: 10.1021/jp0105138.

(3) Stephens, P. J.; McCann, D. M.; Cheeseman, J. R.; Frisch, M. J., "Determination of
absolute configurations of chiral molecules using ab initio time-dependent Density Functional Theory calculations of optical rotation: How reliable are absolute configurations obtained for molecules with small rotations?," Chirality 2005, 17, S52-S64, DOI: 10.1002/chir.20109.

(4) Stephens, P. J.; McCann, D. M.; Devlin, F. J.; Flood, T. C.; Butkus, E.; Stoncius,
S.; Cheeseman, J. R., "Determination of Molecular Structure Using Vibrational Circular Dichroism Spectroscopy: The Keto-lactone Product of Baeyer-Villiger Oxidation of (+)-(1R,5S)-Bicyclo[3.3.1]nonane-2,7-dione," J. Org. Chem. 2005, 70, 3903-3913, DOI: 10.1021/jo047906y.

InChI

1: InChI=1/C7H8O4/c1-10-4-2-3(8)6-7(11-6)5(4)9/h2-3,6-8H,1H3

2: InChI=1/C7H8O4/c8-2-3-1-4(9)6-7(11-6)5(3)10/h1,4,6-9H,2H2

3: InChI=1/C7H8O4/c1-10-4-2-3(8)6-7(11-6)5(4)9/h2,5-7,9H,1H3

Dynamic and non-statistical behavior is the subject of Chapter 7 in my book. Hase and co-workers have uncovered another interesting case of dynamic behavior.¹ The reaction of interest here is F^– + CH₃OOH. A number of different critical points and reactions exist on this surface. The complex CH₃OOH^…F^– (1) lies 36.5 kcal mol^-1 below separated reactants. 1 can rearrange through TS1 (with a barrier of 24.1 kcal mol^-1) to give F^–…CH₃OOH (2). 2 can then cross a second transition state (TS2) with a barrier of 4.7 kcal mol^-1) to give CH₂(OH)₂^…F^– (3), which lies in a very deep well. The B3LYP/6-311+G(d,p) geometries of these critical points are shown in Figure 1.

1 -36.5	TS1 -12.4	2 -16.2
TS2 -11.5	3 -104.8

Figure 1. B3LYP/6-311+G(d,p) optimized geometries of the critical points on the PES for the reaction of F^– with CH₃OOH.¹ Energies in kcal mol^-1 relative to separated reactants

What drew Hase to this problem were the interesting experimental results of Blanksby, Ellison, Bierbaum and Kato.² The gas phase reaction produced HF + CH₂O + OH^–, not 3 or HF + CH₂(OH)O^–. Hase and coworkers ran a number of trajectories simulating reaction at 300 K, the experimental condition. Reactions were started at three points: (1) F^– separated by 15 Å from CH₃OOH, (2) at TS2 or (3) at a point along the intrinsic reaction coordinate (IRC) of the form HOCH₂O^–…HF.

76 of the 80 trajectories that start from TS2 result in the formation of HF + CH₂O + OH^–. The majority of the trajectories that start with separated reactants produce the complex 1 (97 out of 200), reflecting its low energy and high exit barriers. 55 of these200 trajectories remain as isolated reactants. However, 45 trajectories give HF + CH₂O + OH^–, as do all 5 trajectories that start with HOCH₂O^–…HF. No trajectories give 3, the product expected from following the IRC. The computations are in complete agreement with the experimental results; the unusual decomposition products result from following a non-IRC pathway!

Since motion along the imaginary frequency of TS2 initially is to cleave the O-O bond and the C-H bond, momentum in that direction carries the reaction over to the decomposition product rather than making a tight turn on the PES necessary to make 3. These computations show once again that reactions can follow pathways that lie far from steepest descent or IRC pathways.

References

(1) Lopez, J. G.; Vayner, G.; Lourderaj, U.; Addepalli, S. V.; Kato, S.; deJong, W. A.; Windus, T. L.; Hase, W. L., "A Direct Dynamics Trajectory Study of F^– + CH3OOH Reactive Collisions Reveals a Major Non-IRC Reaction Path," J. Am. Chem. Soc. 2007, 129, 9976-9985, DOI: 10.1021/ja0717360.

(2) Blanksby, S. J.; Ellison, G. B.; Bierbaum, V. M.; Kato, S., "Direct Evidence for Base-Mediated Decomposition of Alkyl Hydroperoxides (ROOH) in the Gas Phase," J. Am. Chem. Soc. 2002, 124, 3196-3197, DOI: 10.1021/ja017658c.

I mentioned “mindless chemistry” in the interview with Fritz Schaefer. This term, the title of the article by Schaefer and Schleyer,¹ refers to locating minimum energy structures through a stochastic search driven solely by a computer algorithm. No chemical rationale or intuition is used; rather, the computer simply tries a slew of different possibilities and mindlessly marches through them.

The approach employed by Schaefer and Schleyer is to use the ‘kick” algorithm of Saunders.² An arbitrary initial geometry is first selected (Saunders even suggests the case where all atoms are located at the same point!) and then a kick is applied to each atom, with random direction and displacement, to create a new geometry. An optimization is then performed with some quantum mechanical method, to produce a new structure. The kick is then applied to this new structure (or to the initial one again) to generate another geometry to start up another optimization. By doing many different “kicks” with different kick size, one can span a large swath of configuration space.

In their first “mindless chemistry” paper, Schafer and Schleyer identified some new structures of BCONS, C₆Be and C₆Be^2-.¹ In their next application,³ they explored the novel molecule periodane, which has the molecular formula LiBeBCNOF, named to reflect its make-up of one atom of every element (save neon) on the first full row of the periodic table. Krüger⁴ located the planar structure 1 (see Figure 1). But Schaefer and Schleyer, employing the “kick” algorithm located 27 structures that are lower in energy than 1, Their lowest energy structure 2 is 122 kcal mol^-1 lower than 1. They advocate for this stochastic search to gain broad understanding of the nature of the potential energy surface and then refining the search using “human logic”.

1

2

Figure 1. Optimized structures of periodane 1 and 2.

(Note – I have only provided a sketch of 2 since the supporting information for the article has not yet been posted on the Wiley web site. I will update this post with the actual structure when it becomes available.)

References

(1) Bera, P. P.; Sattelmeyer, K. W.; Saunders, M.; Schaefer, H. F.; Schleyer, P. v. R., "Mindless Chemistry," J. Phys. Chem. A, 2006, 110, 4287-4290, DOI: 10.1021/jp057107z.

(2) Saunders, M., "Stochastic Search for Isomers on a Quantum Mechanical Surface," J. Comput. Chem.. 2004, 25, 621-626, DOI: 10.1002/jcc.10407

(3) Bera, P. P.; Schleyer, P. v. R.; Schaefer, H. F., III, "Periodane: A Wealth of Structural Possibilities Revealed by the Kick Procedure," Int. J. Quantum Chem. 2007, 107, 2220-2223, DOI: 10.1002/qua.21322

(4) Krüger, T., "Periodane – An Unexpectedly Stable Molecule of Unique Composition," Int. J. Quantum Chem. 2006, 106, 1865-1869, DOI: 10.1002/qua.20948

I discuss the concept of σ-aromaticity in Chapter 2.3.1. The arguments for its existence in cyclopropane include surface delocalization of electron density, MO energies, an energetic stability greater than predicted by traditional assessments of its ring strain energy, and a negative value of its NICS(0) and NICS(1).

Fowler, Baker and Lillington have computed the ring current in cyclopropane, cyclobutane and cyclopentane.¹ The later two are computed for their planar conformations, which are not local minima, but make the graphical comparisons simpler. Unfortunately, I do not have electronic access to the journal article and so cannot link to their images, but the plots of the current density of cyclopropane clearly indicates a large diatropic current circling the outside of the ring. In the interior of the ring is a smaller paratropic current.

For this concept to have applicability, cyclobutane should express σ-antiaromaticity. The ring current map for cyclobutane does show a strong paratropic current in the inside of the ring with a weaker diatropic current on the outside of the ring. The current map of cyclopentane shows an interior paratropic and external diatropic currents of nearly identical magnitude, suggestive of a simple superposition of circulation due to five local bonds. Thus, cyclopropane expresses significant σ-aromaticity, cyclobutane is weakly σ-antiaromatic, and cyclopentane is non-aromatic.

References

(1) Fowler, P. W.; Baker, J.; Mark Lillington, M., "The Ring Current in Cyclopropane," Theor. Chem. Acta 2007, 118, 123-127, DOI: 10.1007/s00214-007-0253-2.

InChI:

cyclopropane: InChI=1/C3H6/c1-2-3-1/h1-3H2

cyclobutane: InChI=1/C4H8/c1-2-4-3-1/h1-4H2

cyclopentane: InChI=1/C5H10/c1-2-4-5-3-1/h1-5H2

Despite the fact that Wes Borden has indicated the he has written his last paper on the Cope rearrangement (see my interview with Wes at the end of Chapter 3), others remain intrigued by this reaction and continue to report on it. In a recent JACS communication, Tantillo¹ examines the palladium-promoted Cope rearrangement.

The ordinary Cope rearrangement displays chameleonic character – switching from concerted to stepwise with a diradical intermediate – based on substituents. The palladium-promoted Cope is suggested to proceed through a stepwise mechanism with a zwitterionic intermediate (Scheme 1).²

Scheme 1.

Tantillo¹ has examined a variety of these rearrangements at the B3LYP/LANL2DZ level. The palladium complex is PdCl₂NCMe. For all cases where R is a substituted phenyl group, the mechanism is stepwise, with the intermediate 1 sitting in a shallow well. The most stable intermediate (based on lying in the deepest well) is with the 4-dimethylaminophenyl group, and the well is 5.1 kcal mol^-1 deep. The structures of the transition state (2-pNMe₂) and the intermediate (1-pNMe₂) are shown in Figure 1.

2-pNMe2

1-pNMe2

Figure 1. B3LYP/LANL2DZ optimized structures of 2-pNMe₂ and 1-pNMe₂.¹

However, the well associated with 1 can be very shallow, as little as 0.4 kcal mol^-1 (R = 4-trifluoroimethylphenyl and 4-nitrophenyl). This suggests that perhaps when properly substituted the intermediate might vanish and the reaction become concerted. This is in fact what happens when R is CF₃, CN, or H. The transition state for the reaction with R = H is shown in Figure 2. So, this metal-assisted Cope rearrangement displays chameleonic behavior, just like the metal-free case, except that the intermediate is zwitterionic with the metal, instead of diradical in the metal-free cases.

2-H

Figure 1. B3LYP/LANL2DZ optimized structure of 2-H.¹

References

(1) Siebert, M. R.; Tantillo, D. J., "Transition-State Complexation in Palladium-Promoted [3,3] Sigmatropic Shifts," J. Am. Chem. Soc. 2007, 129, 8686-8687, DOI: 10.1021/ja072159i.

(2) Overman, L. E.; Renaldo, A. E., "Catalyzed Sigmatropic Rearrangements. 10. Mechanism of the Palladium Dichloride Catalyzed Cope Rearrangement of Acyclic Dienes. A Substituent Effect Study," J. Am. Chem. Soc. 1990, 112, 3945-3949, DOI: 10.1021/ja00166a034.

Jorgensen reports an enhanced QM/MM and ab initio study of the rate enhancement of Diels-Alder reactions in various solvents.¹ This study extends earlier studies that he and others have done, many of which are discussed in Chapter 6.2 of the book. In this study, he reports QM/MM computations using the PDDG/PM3 method for the QM component, and MP2 computations incorporating CPCM to account for bulk solvent effects.

The major advance in methodology in this paper is performing a two-dimensional potential of mean force analysis where these two dimensions correspond to the forming C-C distances. In addition, computations were done for water, methanol, acetonitrile and hexane as solvents. Highlights of the results are listed in Table 1.

Table 1. Computed bond asynchronicity^a and activation energy^b (kcal/mol) for the Diels-Alder reaction with cyclopentadiene.

The semi-empirical method underestimates the asynchronicity of these gas-phase Diels-Alder TSs. However, with inclusion of the solvent, the computations do indicate a growing asynchronicity with solvent polarity, This is associated with the ability of the solvent, especially protic solvents, to preferentially hydrogen bond to the carbonyl in the TS.

In terms of energetics, in must first be pointed out that the computations dramatically overestimate the activation barriers. However, the relative trends are reproduced: the barrier increases from water to methanol to acetonitrile to hexane. Jorgensen also computed the activation barriers at MP2/6-311+G(2d,p) with CPCM using the CBS=QB3 gas phase geometries. Some of these results are listed in Table 2. The results for water are in outstanding agreement with experiment. However, the results for the other solvents are poor, underestimating the increase in barrier in moving to the more polar solvent.

Table 2. MP2/6-311+G(2d,p)/CPCM values for ΔG^‡ (kcal/mol).

Bottom line, the conclusions of this study are in agreement with the earlier studies, namely that the hydrophobic effect (better may be the enforced hydrophobic interaction) and greater hydrogen bonding in the TS (both more and stronger hydrogen bonds) account for the rate acceleration of the Diels-Alder reaction in water.

References

(1) Acevedo, O.; Jorgensen, W. L., "Understanding Rate Accelerations for Diels-Alder Reactions in Solution Using Enhanced QM/MM Methodology," J. Chem. Theory Comput. 2007, 3, 1412-1419, DOI: 10.1021/ct700078b.

A couple of additional papers have pointed out systematic problems with using DFT and offer guidelines for methods that provide accurate results. These complement my previous posts on the subject Problems with DFT and Problems with DFT – an Update.

Grimme¹ takes the approach of benchmarking methods and basis sets using isomerization energies, examples of which are shown in Scheme 1. Computed isomerization reaction energies are compared against experimental values or, in a few cases, against extrapolated CCSD(T) energies using cc-pVXZ (X=D-T or X=T-Q). This extrapolation technique² is a way to estimate the complete basis set energy.

Scheme 1.

In terms of basis set, the error systematically decreases with increasing size of the basis set when the SCS-MP2 method is used to compute the energies. Surprisingly, the error is essentially constant for all the basis sets with B3LYP. The root-mean-square deviation and maximum error for the isomerization energies computed with the TZV(2df,2pd) basis set and a variety of different methods are listed in Table 1. Both CCSD(T) and SCS-MP2 provide truly excellent results. Since the later method is much more computationally efficient that the former, Grimme argues that this is really the method of choice for accurate energies. DFT methods vary in their performance, with no discernable trend based on what type of DFT it is (i.e. meta-GGA, hybrid GGA, or hybrid meta-GGA). Of no surprise, based on lots of recent studies (including those blogged about in ), the performance of B3LYP is likely to be problematic.

Table 1. Errors in Computed Isomerization Energies (kcal/mol)

In a related study, Bond³ explores the ability of the composite methods to predict enthalpies and free energies of formation for a set of nearly 300 compounds. Bond makes use of isodesmic and homodesmotic reactions (discussed in Chapter 2). His results for the mean absolute deviations of ΔH are given in Table 2. All of the composite methods (see Chapter 1.2.6) provide quite acceptable results. Once again, B3LYP is shown to be incapable of predicting accurate energies.

Table 2. Mean average deviation in predicted heats of formation compared
to literature values.

References

(1) Grimme, S.; Steinmetz, M.; Korth, M., "How to Compute Isomerization Energies of Organic Molecules with Quantum Chemical Methods," J. Org. Chem., 2007, 72, 2118-2126, DOI: 10.1021/jo062446p.

(2) Helgaker, H.; Klopper, W.; Koch, H.; Noga, J., "Basis-Set Convergence of Correlated Calculations on Water," J. Chem. Phys., 1997, 106, 9639-9646, DOI: 10.1063/1.473863

(3) Bond, D., "Computational Methods in Organic Thermochemistry. 1. Hydrocarbon Enthalpies and Free Energies of Formation," J. Org. Chem. 2007, 72, 5555-5566, DOI: 10.1021/jo070383k

The old EMSL Gaussian Basis Set Order Form (http://www.emsl.pnl.gov/forms/basisform.html) has now been updated to include a very nice interface. The new service is called Basis Set Exchange and is available at https://bse.pnl.gov/bse/portal.

This new service is built off of web 2.0 tools. Most critically, the basis sets are now stored in an XML format that builds upon Chemical Markup Language (CML). Not only can users get a wide variety of basis sets for most elements, basis set developers can upload their basis sets for curation and delivery. The design and implementation of this service is described in a recent article.¹

References

(1) Schuchardt, K. L.; Didier, B. T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T. L., “Basis Set Exchange: A Community Database for Computational Sciences,” J. Chem. Inf. Model 2007, 47, 1045-1052, DOI: 10.1021/ci600510j.