Comparing SN2 and SN1 reactions using computational methods is often quite difficult. The problem is that the heterolytic cleavage in the SN1 reaction leads to an ion pair, and in the gas phase this is a highly endothermic process. Optimization of the ion pair in the gas phase invariably leads to recombination. This is disturbingly the result even when one uses PCM to mimic the solvent, which one might have hoped would be sufficient to stabilize the ions.
The computational study of the glycoside cleavage by Hosoya and colleagues offers some guidance towards dealing with this problem.1 They examined the cleavage of triflate from 2,3,4,6-tetra-O-methyl-α-D-glucopyranosyl triflate 1.
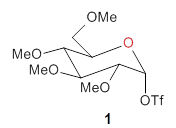
Benchmarking the dissociation energy for the cleavage of 1 and considering computational performance, they settled on M06-2X/BS-III//M06-2X/BS-I, where BS-III is aug-cc-pVTZ basis set for O, F, and Cl and cc-pVTZ for H, C, and S and BS-I is 6-31G(d,p) basis sets were employed for H, C, and S, and 6-31+G(d) for O, F, and Cl. Solvent (dichloromethane) was included through PCM.
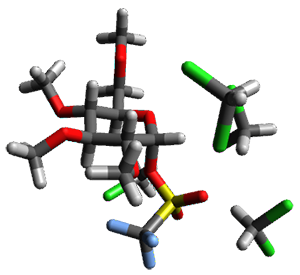
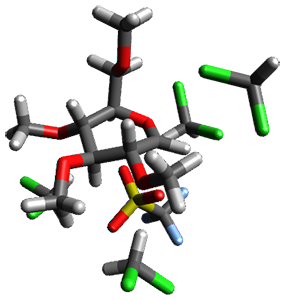
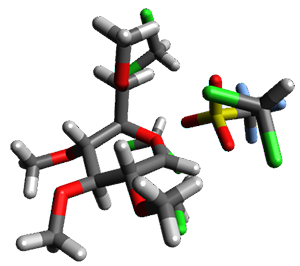
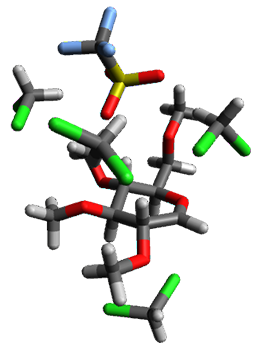
Attempted optimization of the contact ion pair formed from cleavage of 1 invariably led back to the covalent bound 1. PCM is not capable of properly stabilizing these types of ions in proximity. To solve this problem, they incorporated four explicit dichloromethane molecules. A minor drawback to their approach is that they did not sample much of configuration space and so their best geometries may not be the lowest energy configurations. Nonetheless, with four solvent molecules, they were able to locate contact ion pairs and solvent-separated ion pairs. Representative examples are shown in Figure 1. This method of explicit incorporation of a few solvent molecules seems to be the direction we must take to treat ions or even highly polar molecules in solution.
|
1 |
1-CIP |
|
1-SSIPa |
Figure 1. Representative examples of microsolvated 1, its contact ion pair (CIP) and solvent separated ion pair (SSIP) computed at M06-2X/BS-III//M06-2X/BS-I, and relative energies (kcal mol-1)
References
(1) Hosoya, T.; Takano, T.; Kosma, P.; Rosenau, T. "Theoretical Foundation for the Presence of Oxacarbenium Ions in Chemical Glycoside Synthesis," J. Org. Chem. 2014, 79, 7889-7894, DOI: 10.1021/jo501012s.
InChIs
1: InChI=1S/C11H19F3O8S/c1-17-5-6-7(18-2)8(19-3)9(20-4)10(21-6)22-23(15,16)11(12,13)14/h6-10H,5H2,1-4H3/t6-,7-,8+,9-,10-/m1/s1
InChIKey=RPZNYYCDDYUPJR-HOTMZDKISA-N

Henry Rzepa responded on 06 Nov 2014 at 3:15 am #
I think the concept that continuum solvation on its own is insufficient to characterise separated (or contact) ion pairs has been known for a little while.
Thus in doi:10.1021/jo100920e it is commented that the addition of discrete solvent molecules to the continuum model is required to reproduce experimental behaviour.
In 1991, the (known) thermodynamics of the ionisation of glycine into a zwitterion could only be reproduced by constructed a model with continuum solvation and (about 16) discrete solvent molecules, see doi:10.1039/P29910000531.
Both these models used water as discrete solvent embedded in a continuum solvent field, and so it is interesting to see that this behaviour also extends to less polar solvents such as DCM.
Henry Rzepa responded on 06 Nov 2014 at 3:45 am #
Here are some results I reported at WATOC 2011: http://www.ch.ic.ac.uk/rzepa/talks/watoc11/2a.html for glycine.
The reported equilibrium constant for glycine in water favours the zwitterion by about -8 to -10 kcal/mol, with an entropy of -7.5 cal mol-1 K-1. Gas phase gets it at about +27.7 for the free energy, a gas phase model with 7H2O reduces it to about -11 but the entropy is not quite correct. A continuum field on the other hand is only +5.5 kcal/mol (and this included full geometry re-optimisation in that field). The combined model is -11, and the entropy -9, which is fairly close. All the original calculations are archived on our DSpace repository, if anyone wants to take a look (the links are from the slide above, eg http://doi.org/10042/to-8993).
Given that the density of states for how 7H2O might orient around the glycine is quite high, one must treat the entropy with caution, but it does illustrate how poor the continuum models can be. In this case of course it is due to explicit hydrogen bonds forming, which the continuum method does not model. But I guess even with dichloromethane, there must be (weaker) hydrogen bonds being formed which are not handled by the continuum method. I will report an NCI analysis of the systems Steve notes above to see what that shows.
Henry Rzepa responded on 06 Nov 2014 at 3:54 am #
One more comment. Treating the (solvated) potential energy surface is crucial for other techniques such as IRC (intrinsic reaction coordinates). The classical solvolysis of t-butyl chloride in water is much studied. A gas phase model will not produce anything like a sensible IRC. But a continuum model with 16 discrete water molecules certainly does better, see http://www.ch.imperial.ac.uk/rzepa/blog/?p=5228
In fact, the solvent separated ion pair is characterised only as a hidden intermediate, since eventually attack by one of the water molecules on the t-butyl carbocation occurs. But the IRC shows a long period whilst the solvent-separated ion pair (almost) forms.
No IRCs are reported in 10.1021/jo501012s and it would be highly desirable to see what they look like! I repeat, sensible IRCs for reactions involving ion pairs are only obtained with a combination of discrete molecule and continuum solvent models.
Jan Jensen responded on 06 Nov 2014 at 4:17 am #
There’s also these ways of determining the optimum number of explicit solvent molecules for a solute: 10.1021/jp802665d
Henry Rzepa responded on 06 Nov 2014 at 1:18 pm #
An NCI analysis of 1 and SSIP can be viewed here. It is one technique that can differentiate between relatively strong directional interactions (hydrogen bonds) and the weaker less directional dispersion terms.
The solvation of ion pairs. « Henry Rzepa's blog responded on 08 Jul 2015 at 10:52 am #
[…] methods has been a challenging business. This post was inspired by reading Steve Bachrach’s post, itself alluding to this aspect in the title “Computationally handling ion pairs”. It […]