The most favorable conformation of a carboxylic acid is the Z form. In fact, the E form is rarely found. Schreiner now offers an explanation for why this is so.¹

Photolysis of matrix-deposited benzoic acid revealed only the Z form (1Z). However, photolysis of deuterated benzoic acid did reveal the E form 1E, however it disappeared with a half-life of 12 minutes on argon at 11 K and 20 K. The lack of temperature dependence, and the huge isotope effect suggested that the isomerization proceeds via tunneling.

The tunneling rate was computed by generating the reaction path at CCSD(T)/cc-pVTZ with
MP2/cc-pVDZ zero point energy. This gave a half-life of 2.8 h for the deuterium species and 10^-5 min for the proton species. A Hammet-like relationship could be produced for the half-lives of para-substituted benzoic acids. Interestingly, a nice correlation is found between the computed width of the tunneling barrier and the half life with σ-donating ability.

References

(1) Amiri, S.; Reisenauer, H. P.; Schreiner, P. R., "Electronic Effects on Atom Tunneling: Conformational Isomerization of Monomeric Para-Substituted Benzoic Acid Derivatives," J. Am. Chem. Soc., 2010, 132 , 15902–15904, DOI: 10.1021/ja107531y

InChIs

Benzoic acid: InChI=1/C7H6O2/c8-7(9)6-4-2-1-3-5-6/h1-5H,(H,8,9)/f/h8H
InChIKey=WPYMKLBDIGXBTP-FZOZFQFYCI

Somehow I missed this paper when it came out a few months ago, even though I was aware it was coming – as I mentioned it in one of my previous posts!

Anyways, Schreiner and Allen reported on their third study of hydroxyl carbenes (see these posts on dihydroxymethylene and hydroxymethylene), this time examining phenylhydroxycarbene.¹ As I covered in my book, there is a lot of work on phenylcarbenes which typically ring expand to the cycloheptatetraene, see Reaction 1. One might expect phenylhydroxycarbene to do the same thing, i.e. 1 converting into 2 (Reaction 2). 1 is prepared by high-vacuum flash pyrolysis of phenylglyoxylic acid 3 and then capturing the product in an argon matrix at 11 K (Reaction 3).

The carbene 1 is identified through comparison of its experimental and computed (anharmonic frequencies at CCSD(T)/cc-pVDZ) IR frequencies.

No ring expansion is observed at all – Reaction 2 does not occur. Instead, 1 rearranges to benzaldehyde 4 (Reaction 4) at 11 K with a half life of 2.46 h (and a half life of 2.55 h at 20 K). The deuterated analogue does not convert to benzaldehyde and 1-d appears to be completely stable.

So, what is going on? The cis and trans forms of 1 interconvert through a barrier of 22.7 kcal mol^-1. The trans isomer can convert to benzaldehyde (the reaction is very exothermic: -50.8 kcal mol^-1) with a barrier of 28.8 kcal mol^-1 through TS1, shown in Figure 1. The cis isomer can cleave into benzene and CO (not observed) with a huge barrier of 55 kcal mol^-1. All of these barrier were computed at CCSD(T)/cc-pVQZ.

TS1

Figure 1. MP2/cc-pVDZ optimized transition state for the conversion of 1 into 4.

Benzaldehyde seems to be produced by passing through a huge barrier, something that is impossible from a thermal perspective (we’re at 11 K!). But this can be accomplished by tunneling. Tunneling probabilities were computed from the MP2/aug-cc-pVDZ intrinsic reaction path with barrier penetration integrals computed with the WKB approximation. The bottom line: the computed half-life is 3.3 h and the deuterated species is computed to have a half-life of 8700 years(!), both in excellent agreement with experimental observation. Quantum mechanical tunneling is clearly the explanation for this chemistry.

This is another fine example of the power of joint experimental/computational studies. And be on the look-out for an even more exciting case from this group. I met with Wes Allen on my recent trip to the University of Georgia and was entertained with another hydroxycarbene that undergoes quite novel tunneling!

References

(1) Gerbig, D.; Reisenauer, H. P.; Wu, C.-H.; Ley, D.; Allen, W. D.; Schreiner, P. R., "Phenylhydroxycarbene," J. Am. Chem. Soc., 2010, 132, 7273-7275, DOI: 10.1021/ja9107885

InChIs

1: InChI=1/C7H6O/c8-6-7-4-2-1-3-5-7/h1-5,8H
InChIKey=QVZIGMRPQWIGCV-UHFFFAOYAE

2: InChI=1/C7H6O/c8-7-5-3-1-2-4-6-7/h1-6H
InChIKey=QVWDCTQRORVHHT-UHFFFAOYAM

3: InChI=1/C8H6O3/c9-7(8(10)11)6-4-2-1-3-5-6/h1-5H,(H,10,11)/f/h10H
InChIKey=FAQJJMHZNSSFSM-KZFATGLACS

4: InChI=1/C7H6O/c8-6-7-4-2-1-3-5-7/h1-6H
InChIKey=HUMNYLRZRPPJDN-UHFFFAOYAE

Not particularly strong programming at the year’s spring ACS meeting – but one great session in the organic division yesterday. This was the awards session in honor of John Baldwin getting the James Flack Norris Award for physical organic chemistry.

First to speak was James Duncan, who discussed his recent CASSCF computations looking for pseudopericylic [3,3]-sigmatropic migrations. I will be commenting on his latest work in a post that will appear soon.

I had to skip the next talk, but came back to hear John Brauman discuss recent work on the solvation effect in the S_N2 reaction. This is an interesting case of where the screening of larger substituents is counterbalanced by geometric changes that lead to greater charge distribution. The net effect is that they cancel each other out, and the methyl,ethyl, iso-propyl, butyl β-effect is negligible.

Next was Peter Schreiner who discussed his carbene work, specifically the enormous tunneling effect observed in hydroxymethylene (see this post). He discussed some new work, that is if anything even more fantastic on methylhydroxycarbene – look for this work perhaps later in 2011.

Last to speak was John Baldwin – and he described his truly tour de force efforts in examining the [1,3]-rearrangements of vinylcyclopropane and vinylcyclobutane. The former work is described in my book, while the later study is still ongoing.

John’s work is amazingly painstaking and careful. I am truly in awe of his dedication in taking on extremely difficult studies that require enormous care. John has really taught us a lot – not just about these rearrangements (they involve diradicals on a flat plateau demanding dynamic analysis – but how to think about a study and then carry it out to fruition so that all details are assessed. A truly deserving recipient!

Does the Carbon-Sulfur triple bond exist? There’s probably little doubt it does in the CS molecule. But now Schreiner and Mloston have offered up the H-C≡S-OH species as a possibility.¹ Obtained by flash photolysis of 1, giving 2, and upon irradiation at 254 nm, H-C≡S-OH 3 is the observed species and not the expected carbene HO-C-SH 4. 3 is confirmed by excellent agreement between the observed and computationally predicted IR spectra.

The CCSD(T)/cc-pVTZ structures of 3 and 4 are shown in Figure 1. It is interesting that the carbene is not observed, even though it is 26.6 kcal mol^-1 more stable than 3.

3

4

Figure 1. CCSD(T)/cc-PVTZ optimized structures of 3 and 4.¹

So is there a triple bond? The short C-S distance (1.547 Å) is very similar to that in CS (1.545 Å). NBO analysis indicates a triple bond. But the MOs indicate significant lone pair build-up on both C and S, consistent with the strongly non-linear angles about these two atoms. The authors conclude that 3 is a “structure with a rather strong CS double bond or a weak triple bond”.

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Romanski, J.; Mloston, G., "A Formal Carbon-Sulfur Triple Bond: H-C≡S-O-H," Angew. Chem. Int. Ed., 2009, 48, 8133-8136, DOI: 10.1002/anie.200903969

Following on the great study of hydroxycarbene¹ (see my blog post), Schreiner now reports on the synthesis and characterization of dihydroxycarbene 1.² It is prepared by high-vacuum flash pyrolysis of oxalic acid (Scheme 1).

Scheme 1

Dihydroxycarbene can exist in three different conformations characterized by the relationship about the C-O bond, either s-cis or s-trans. The three conformations are shown in Figure 1, and the s-trans,s-trans structure is the local energy minimum (computed at CCSD(T)/cc-pVTZ).

1tt (0.0)

1ct (0.1)

1cc (6.7)

Figure 1. CCSD(T)/cc-pVTZ optimized geometries and relative energies (kcal mol^-1) of the conformers of 1.²

Identification of the 1 is made through comparison of the experimental and computed IR vibrational frequencies. As an example, the experimental and computed frequencies for the s-trans,s-trans conformer are listed in Table 1. The agreement is excellent.

Table 1. Computed and experimental vibrational frequencies (cm^-1) and intensities (in parentheses) of the s-trans,s-trans conformation of 1.²

Unlike hydroxycarbene, dihydroxycarbene is stable. The amazing instability of hydroxycarbene is due to tunneling through a large barrier: nearly 30 kcal mol^-1.¹ The tunneling route for the decomposition of 1 is more difficult for two reasons. First, its C-O bond is quite strong; the C-O distance is quite short, 1.325 Å. This makes a long distance that must be traversed in the tunneling mode. (The strong bond is due to π-donation from the oxygen lone pair into the empty carbon p orbital; this is noted by the large rotational barrier about the C-O bonds of 17 kcal mol^-1!) Second, the activation barrier for decomposition is very high, at least 34 kcal mol^-1.

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Pickard Iv, F. C.; Simmonett, A. C.; Allen, W. D.; Matyus, E.; Csaszar, A. G., "Capture of hydroxymethylene and its fast disappearance through tunnelling," Nature, 2008, 453, 906-909, DOI: 10.1038/nature07010.

(2) Schreiner, P. R.; Reisenauer, H. P., "Spectroscopic Identification of Dihydroxycarbene13," Angew. Chem. Int. Ed., 2008, 47, 7071-7074, DOI: 10.1002/anie.200802105

InChIs

1: InChI=1/CH2O2/c2-1-3/h2-3H

A nice summary of the tunneling behavior of hydroxymethylene¹ was just published by Bucher in Angewandte Chemie.² Bucher strongly points out that the really novel part of this work is the very large barrier through which the proton tunnels. My blog post on this topic is here.

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Pickard IV, F. C.; Simmonett, A. C.; Allen, W.
D.; Matyus, E.; Csaszar, A. G., "Capture of hydroxymethylene and its fast disappearance through tunnelling," Nature, 2008, 453, 906-909, DOI: 10.1038/nature07010.

(2) Bucher, G.; “Hydroxycarbene: Watching a Molecular Mole at Work,” Angew. Chem. Int. Ed., 2008, 47, 6957 – 6958, DOI: 10.1002/anie.200803195

The very simple carbene hydroxymethylene, HOCH, has finally been prepared and characterized.¹ Glyoxylic acid CHOCO₂H is subjected to high-vacuum laser photolysis. It fragments into HOCH, which is then trapped into an argon matrix. The experimental IR frequencies match up very well with the CCSD(T)/cc-pVQZ harmonic frequencies of the trans isomer 1t that are also adjusted for anharmonic effects. The computed vertical excitation energy of 415 nm matches well with the experimental value of the maximum absorption in the UV/vis spectra of 427 nm.

The other very interesting experimental result is that HOCH has a lifetime of about 2 hours in the matrix, while the deuterated species DOCH is stable. To explain these results, Schreiner, Allen and co-workers optimized a number of structures on the PES at CCSD(T)/cc-pVQZ and computed their energies using the focal point technique. The optimized structures and their relative energies are given in Figure 1.

1t (0.0)	TS2 (29.7)	2 (-52.1)
TS1(26.8)
1c (4.4)

Figure 1. Optimized CCSD(T)/cc-pVQZ structures of HOCH isomers and their Focal Point relative energies (kcal mol^-1).¹

The barriers for rearrangement from 1t are both very high. Rearrangement to formaldehyde 2 requires crossing a barrier of 29.7 kcal mol^-1, while the barrier to convert to the cis isomer 1c is 26.8 kcal mol^-1. (Note that from 1c a cleavage into CO and H2 can occur, but this barrier is another 47.0 kcal mol^-1.) These barriers are too large to be crossed at the very low temperatures of the matrices. However, using the intrinsic reaction potential at CCSD(T)/cc-pVQZ and WKB theory, the tunneling lifetime of HOCH is computed to be 122 minutes, in excellent accord with the experiment. The lifetime for DOCH is computed to be over 1200 years. Thus, the degradation of hydroxymethylene is entirely due to tunneling through a very large classical barrier! This rapid tunneling casts serious doubt on the ability to ever identify any hydroxymethylene in interstellar space.

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Pickard IV, F. C.; Simmonett, A. C.; Allen, W.
D.; Matyus, E.; Csaszar, A. G., "Capture of hydroxymethylene and its fast disappearance through tunnelling," Nature, 2008, 453, 906-909, DOI: 10.1038/nature07010.

InChI

1: InChI=1/CH2O/c1-2/h1-2H
2: InChI=1/CH2O/c1-2/h1H2

I just ran across a nice summary article by Peter Schreiner¹ detailing the recent spate of articles describing problems with many DFT methods, especially the ubiquitous B3LYP functional. This article covers essentially the same ground as my previous post Problems with DFT.

References

(1) Schreiner, P. R., “Relative Energy Computations with Approximate Density Functional Theory – A Caveat!,” Angew. Chem. Int. Ed., 2007, 46, 4217-4219, DOI: 10.1002/anie.200700386.

We noted in Chapter 2.1 some serious errors in the prediction of bond dissociation energies using B3LYP. For example, Gilbert examined the C-C bond dissociation energy of some simple branched alkanes.¹ The mean absolute deviation (MAD) for the bond dissociation energy predicted by G3MP2 is 1.7 kcal mol^-1 and 2.8 kcal mol^-1 using MP2. In contrast, the MAD for the B3LYP predicted values is 13.7 kcal mol^-1, with some predictions in error by more than 20 kcal mol^-1. Furthermore, the size of the error increases with the size of the molecule. Consistent with this trend, Curtiss and co-workers noted a systematic underestimation of the heat of formation of linear alkanes of nearly 0.7 kcal mol^-1 per bond using B3LYP.²

Further evidence disparaging the general performance of DFT methods (and B3LYP in particular) was presented in a paper by Grimme and in two back-to-back Organic Letters articles, one by Schreiner and one by Schleyer. Grimme³ noted that the relative Energy of two C₈H₁₈ isomers, octane and 2,2,3,3-tetramethylbutane are incorrectly predicted by DFT methods (Table 1). While MP2 and CSC-MP2 (spin-component-scaled MP2) correctly predict that the more branched isomer is more stable, the DFT methods predict the inverse! Grimme attributes this error to a failure of these DFT methods to adequately describe medium-range electron correlation.

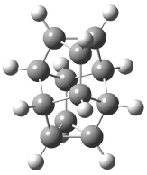
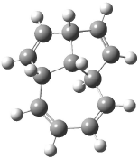
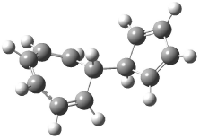
Schreiner⁵ also compared the energies of hydrocarbon isomers. For example, the three lowest energy isomers of C₁₂H₁₂ are 1-3, whose B3LYP/6-31G(d) structures are shown in Figure 1. What is disturbing is that the relative energies of these three isomers depends strongly upon the computational method (Table 2), especially since these three compounds appear to be quite ordinary hydrocarbons. CCSD(T) predicts that 2 is about 15 kcal mol^-1 less stable than 1 and that 3 lies another 10 kcal mol^-1 higher in energy. MP2 exaggerates the separation by a few kcal mol^-1. HF predicts that 1 and 2 are degenerate. The large HF component within B3LYP leads to this DFT method’s poor performance. B3PW91 does reasonably well in reproducing the CCSD(T) results.

1 xyz file

2 xyz file

3 xyz file

Figure 1. Structures of 1-3 at B3LYP/6-31G(d).

Another of Schreiner’s examples is the relative energies of the C₁₀H­₁₀ isomers; Table 3 compares their relative experimental heats of formation with their computed energies. MP2 adequately reproduces the isomeric energy differences. B3LYP fairs quite poorly in this task. The errors seem to be most egregious for compounds with many single bonds. Schreiner recommends that while DFT-optimized geometries are reasonable, their energies are unreliable and some non-DFT method should be utilized instead.

Schleyer’s example of poor DFT performance is in the isodesmic energy of Reaction 1 evaluated for the n-alkanes.⁶ The energy of this reaction becomes more positive with increasing chain length, which Schleyer attributes to stabilizing 1,3-interactions between methyl or methylene groups. (Schleyer ascribes the term “protobranching” to this phenomenon.) The stabilization energy of protobranching using experimental heats of formation increases essentially linearly with the length of the chain, as seen in Figure 2.

n-CH₃(CH₂)_mCH₃ + mCH₄ → (m + 1)C₂H₆         Reaction 1

Schleyer evaluated the protobranching energy using a variety of methods, and these energies are also plotted in Figure 2. As expected, the G3 predictions match the experimental values quite closely. However, all of the DFT methods underestimate the stabilization energy. Most concerning is the poor performance of B3LYP. All three of these papers clearly raise concerns over the continued widespread use of B3LYP as the de facto DFT method. Even the new hybrid meta-GGA functionals fail to adequately predict the protobranching phenomenon, leading Schleyer to conclude: “We hope that Check and Gilbert’s pessimistic admonition that ‘a computational chemist cannot trust a one-type DFT calculation’¹ can be overcome eventually”. These papers provide a clear challenge to developers of new functionals.

Figure 2. Comparison of computed and experimental protobranching stabilization energy (as defined in Reaction 1) vs. m, the number of methylene groups of the n-alkane chain.⁶

Truhlar believes that one of his newly developed functionals answers the call for a reliable method. In a recent article,⁴ Truhlar demonstrates that the M05-2X⁷ functional performs very well in all three of the cases discussed here. In the case of the C₈H₁₈ isomers (Table 1), M05-2X properly predicts that 2,2,3,3-tetramethylbutane is more stable than octane, and estimates their energy difference within the error limit of the experiment. Second, M05-2X predicts the relative energies of the C₁₂H₁₂ isomers 1-3 within a couple of kcal mol^-1 of the CCSD(T) results (see Table 2). Last, in evaluating the isodesmic energy of Reaction 1 for hexane and octane, M05-2X/6-311+G(2df,2p) predicts energies of 11.5 and 17.2 kcal mol^-1 respectively. These are in excellent agreement with the experimental values of 13.1 kcal mol^-1 for butane and 19.8 kcal mol^-1 for octane.

Truhlar has also touted the M05-2X functional’s performance in handling noncovalent interactions.⁸ For example, the mean unsigned error (MUE) in the prediction of the binding energies of six hydrogen-bonded dimers is 0.20 kcal mol^-1. This error is comparable to that from G3 and much better than CCSD(T). With the M05-2X functional already implemented within NWChem and soon to be released within Gaussian and Jaguar, it is likely that M05-2X may supplant B3LYP as the new de facto functional in standard computational chemical practice.

Schleyer has now examined the bond separation energies of 72 simple organic molecules computed using a variety of functionals,⁹ including the workhorse B3LYP and Truhlar’s new M05-2X. Bond separation energies are defined by reactions of each compound, such as three shown below:

The new M05-2X functional performed the best, with a mean absolute deviation (MAD) from the experimental energy of only 2.13 kcal mol^-1. B3LYP performed much worse, with a MAD of 3.96 kcal mol^-1. As noted before, B3LYP energies become worse with increasing size of the molecules, but this problem is not observed for the other functionals examined (including PW91, PBE, and mPW1PW91, among others). So while M05-2X overall appears to solve many of the problems noted with common functionals, it too has some notable failures. In particular, the error is the bond separation energies of 4, 5, and 6 is -8.8, -6.8, and -6.0 kcal mol^-1, respectively.

References

(1) Check, C. E.; Gilbert, T. M., “Progressive Systematic Underestimation of Reaction Energies by the B3LYP Model as the Number of C-C Bonds Increases: Why Organic Chemists Should Use Multiple DFT Models for Calculations Involving Polycarbon Hydrocarbons,” J. Org. Chem. 2005, 70, 9828-9834, DOI: 10.1021/jo051545k.

(2) Redfern, P. C.; Zapol, P.; Curtiss, L. A.; Raghavachari, K., “Assessment of Gaussian-3 and Density Functional Theories for Enthalpies of Formation of C₁-C₁₆ Alkanes,” J. Phys. Chem. A 2000, 104, 5850-5854, DOI: 10.1021/jp994429s.

(3) Grimme, S., “Seemingly Simple Stereoelectronic Effects in Alkane Isomers and the Implications for Kohn-Sham Density Functional Theory,” Angew. Chem. Int. Ed. 2006, 45, 4460-4464, DOI: 10.1002/anie.200600448

(4) Zhao, Y.; Truhlar, D. G., “A Density Functional That Accounts for Medium-Range Correlation Energies in Organic Chemistry,” Org. Lett. 2006, 8, 5753-5755, DOI: 10.1021/ol062318n

(5) Schreiner, P. R.; Fokin, A. A.; Pascal, R. A.; deMeijere, A., “Many Density Functional Theory Approaches Fail To Give Reliable Large Hydrocarbon Isomer Energy Differences,” Org. Lett. 2006, 8, 3635-3638, DOI: 10.1021/ol0610486

(6) Wodrich, M. D.; Corminboeuf, C.; Schleyer, P. v. R., “Systematic Errors in Computed Alkane Energies Using B3LYP and Other Popular DFT Functionals,” Org. Lett. 2006, 8, 3631-3634, DOI: 10.1021/ol061016i

(7) Zhao, Y.; Schultz, N. E.; Truhlar, D. G., “Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions,” J. Chem. Theory Comput. 2006, 2, 364-382, DOI: 10.1021/ct0502763.

(8) Zhao, Y.; Truhlar, D. G., “Assessment of Model Chemistries for Noncovalent Interactions,” J. Chem. Theory Comput. 2006, 2, 1009-1018, DOI: 10.1021/ct060044j.

(9) Wodrich, M. D.; Corminboeuf, C.; Schreiner, P. R.; Fokin, A. A.; Schleyer, P. v. R., “How Accurate Are DFT Treatments of Organic Energies?,” Org. Lett., 2007, 9, 1851-1854, DOI: 10.1021/ol070354w.

InChI

1: InChI=1/C11H10/c1-2-5-7-3(1)4(1)8-6(2)10-9(5)11(7,8)10/h1-10H

2: InChI=1/C12H12/c1-2-4-10-6-8-11-7-5-9(3-1)12(10)11/h1-12H

3: InChI=1/C12H12/c1-2-4-8-11(7-3-1)12-9-5-6-10-12/h1-12H

4: InChI=1/C6H6/c1-4-5(2)6(4)3/h1-3H2

5: InChI=1/C8H10/c1-3-7-5-6-8(7)4-2/h3-4H,1-2,5-6H2

6: InChI=1/C10H10/c1-2-8-5-6-9-4-3-7(1)10(8)9/h1-10H