If you hadn’t noticed, I am a big fan of the work that Dan Singleton is doing concerning the role of dynamics in discerning reaction mechanisms. Dan’s group has reported another outstanding study combining experiments, traditional QM computations, and molecular dynamics – this time on the Wittig reaction.¹

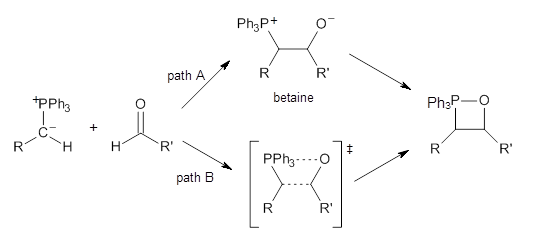
The key question concerning the mechanism is whether a betaine intermediate is accessed along the reaction (path A) or whether the reaction proceeds in a concerted manner (path B). Earlier computations had supported the concerted pathway (B).

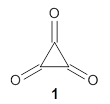
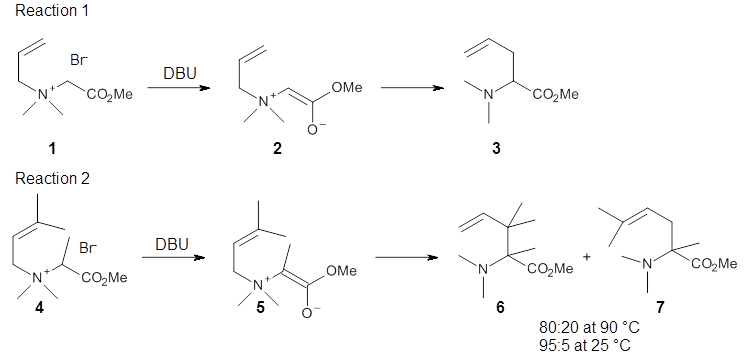
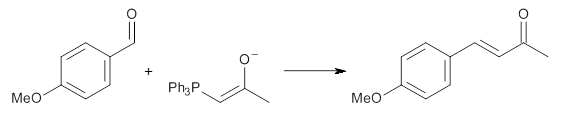
Experimental determination of the heavy atom kinetic isotope effect was made for Reaction 1.

Reaction 1

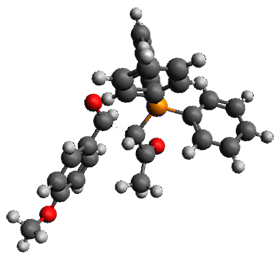
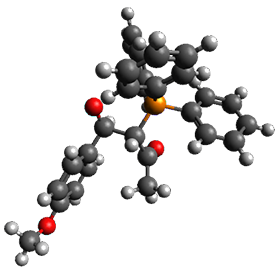
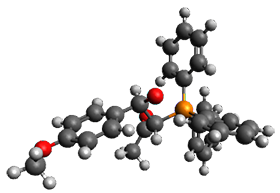
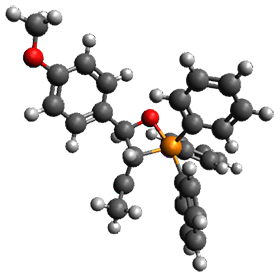
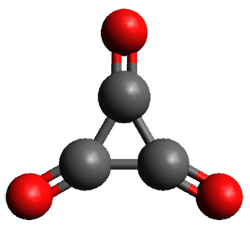
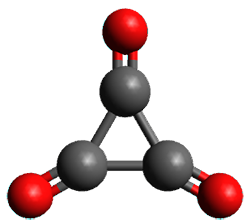
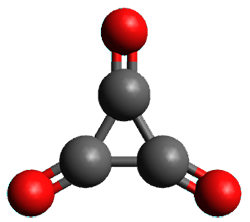
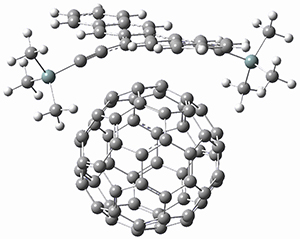
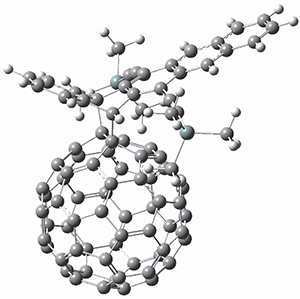
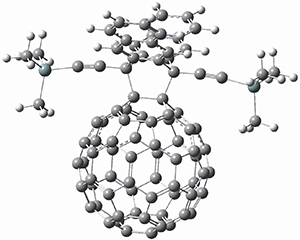
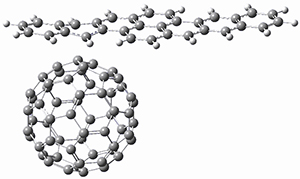
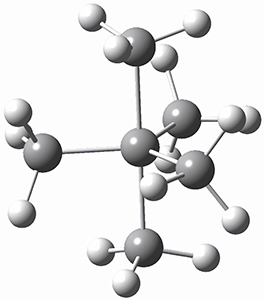
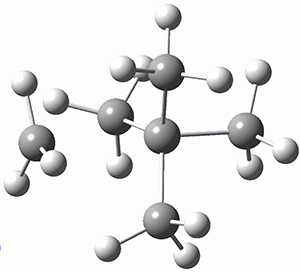
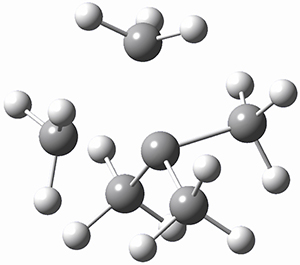
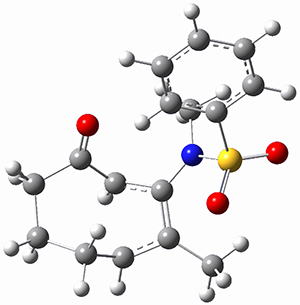
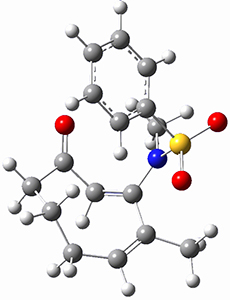
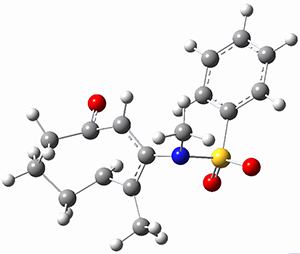
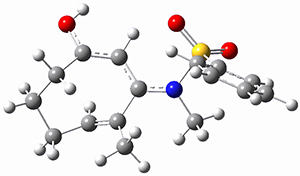
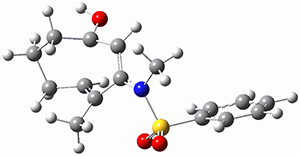
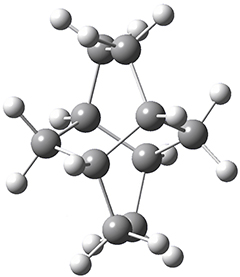
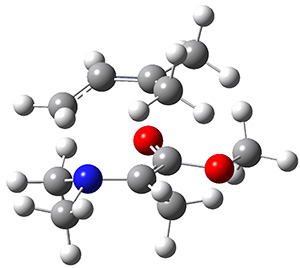
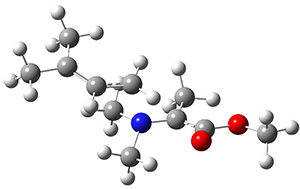
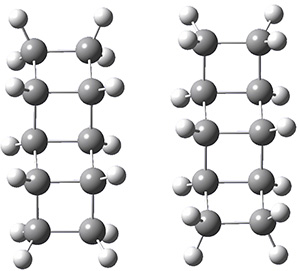
Using the 6-31+G(2df,p) basis set, three different density functionals predict three different potential energy surfaces. With M06-2x, the surface indicates path A (stepwise), with the first step rate-limiting. B3P86 also predicts the stepwise reaction, but the second step is rate-limiting. The Lc-wPBE functional predicts a concerted reaction. Using these surfaces, they predicted the carbon isotope effect and compared it to the experimental values. The best agreement is with the M06-2x surface with a weighting of the vibrational energies of the two different TSs. The optimized structures of the two transition states, the betaine intermediate, and the product are shown in Figure 1.

TS1	Betaine
TS2	Product

Figure 1. M06-2x/6-31+G(2df,p) optimized geometry of the critical points of Reaction 1.

The agreement of the predicted and experimental KIE is not ideal. So, they performed molecular dynamics computations with the ONIOM approach using M06-2x/6-31G* for Reaction 1 and 53 THF molecules treated at PM3. 360 trajectories were begun in the region of the first transition state (TS1), and they can be organized into 4 groups. The first group (128 trajectories) are reactions that produce product. The second group (76 cases) form the C-C bond but then it ruptures and returns to reactant. The third group (82 cases) have an immediate recrossing back to reactant, and the last group (16 cases) takes product back to the first TS and then returns to product. The predicted KIE using this weighted MD results gives values in outstanding agreement with the experiments.

Of the first group, about 50% pass from TS1 to TS2 in less than 150 fs, or in other words look like a concerted path. But a good number of trajectories reside in the betaine region for 1-2 ps.

In contrast, trajectories initiated from the betaine with equilibrated THF molecules indicate a median of 600 ps to travel from TS1 to TS2 and do not resemble a concerted path.

They argue that this bimodal distribution is in part associated with a solvent effect. When the first TS is crossed the solvent molecules are not equilibrated about the solute, and 10-20% of the trajectories immediately pass through the betaine region due to “dynamic matching” where the entering motion matches with exiting over the second transition state. The longer trajectories result from improper dynamic matching, but faster motion in the solute than motion amongst the solvent needed to stabilize the betaine. So, not only do we need to be concerned about dynamic effects involving the reactants, we need to be concerned about dynamics associated with the solvent too!

References

(1) Chen, Z.; Nieves-Quinones, Y.; Waas, J. R.; Singleton, D. A. "Isotope Effects, Dynamic Matching, and Solvent Dynamics in a Wittig Reaction. Betaines as Bypassed Intermediates," J. Am. Chem. Soc. 2014, 136, 13122-13125, DOI: 10.1021/ja506497b.

As recently explicated by Wang and Borden using NIPE spectroscopy and computations, the potential energy surface of cyclopropyl-1,2,3-trione 1 is remarkably complex.¹ (U)CCSD(T)//aug-cc-pVTZ computations of the D_3h singlet (the ¹A_1’ state shown in Figure 1) is actually a hilltop, possessing two imaginary frequencies. Distorting the structure as indicated by these imaginary frequencies and then optimizing the structure leads directly to dissociation to three CO molecules. Thus, (CO)₃ does not exist as a stable minima on the singlet surface.

The D_3h triplet (the ³E” state shown in Figure 1) is not a critical point on the surface; due to the Jahn-Teller effect is distorts into two different states: the ³B₁ state which is a local energy minimum, and the ³A₂ state which is a transition state between the symmetry-related ³B₁ states.

So, this implies the possibility of a very interesting NIPE experiment. If the radical anion (CO)₃^-.
loses an electron and goes to the singlet surface, it lands at a hilltop(!) and should have a very short lifetime. If it goes to the triplet surface, it lands at either a transition state (³A₂) and again should have a short lifetime, or it can land at the ³B₁ state and perhaps have some lifetime before it dissociates by losing one CO molecule.

1-.
1A1’	3E”
3B1	3A2

Figure 1. (U)CCSD(T)//aug-cc-pVTZ optimized geometries of 1 and its radical anion.

The NIPE spectrum identifies three transitions. By comparing the energies of the electron loss seen in the experiment with the computations, along with calculating the Franck-Condon factors using the computed geometries and vibrational frequencies, the lowest energy transition is to the ¹A_1’ state, and the second transition is part of the vibrational progression also to the ¹A_1’ state. This is the first identification of vibrational frequencies associated with a hilltop structure. The third transition is to the ³A₂ state. No transition to the ³B₁ state is found due to the large geometric difference between the radical anion and the ³B₁ state; the Franck-Condon factors are zero due to no overlap of their wavefunctions.

Once again, the power of the symbiotic relationship between experiment and computation is amply demonstrated in this paper.

References

(1) Chen, B.; Hrovat, D. A.; West, R.; Deng, S. H. M.; Wang, X.-B.; Borden, W. T. "The Negative Ion Photoelectron Spectrum of Cyclopropane-1,2,3-Trione Radical Anion, (CO)₃^•– — A Joint Experimental and Computational Study," J. Am. Chem. Soc. 2014, 136, 12345-12354, DOI: 10.1021/ja505582k.

InChIs

1: InChI=1S/C3O3/c4-1-2(5)3(1)6
InChIKey=RONYDRNIQQTADL-UHFFFAOYSA-N

Diels-Alder reaction involving fullerenes have been known for some time. They occur across the [6,6] double bond of C₆₀, the one between two fused 6-member rings. Houk and Briseno report on the Diels-Alder reaction of C₆₀ with pentacene 1 and bistetracene 2 and compare their computations with experiments.¹

Pentacene and bistetracene ring numbering convention

Computations were performed for the reaction of 1 and 2 with C₆₀ at M06-2x/6-31G(d)//M062x-3-21G*. The reaction can occur with the dienophile being either ring 1, 2, or 3 of pentacene and ring 1, 2, 3, or 4 of bistetracene. They located TSs and products for all of these possibilities. Select TSs and products are shown in Figure 1.

For the reaction of 1a, the lowest energy TS is for the reaction at the central ring (ring 3), and the resulting product is the lowest energy product. The transition state (PT_TS3) is shown in Figure 1. This TS has the least distortion energy of the three possibilities, because reacting at this central ring destroys the least amount of aromaticity of pentacene. For the reaction of 1b, the lowest barrier is again for reaction of ring 3 (through TMSPT_TS3). However, the product from the reaction with ring 2 (TMSPT_P2) is lower in free energy than TMSPT­_P3, likely caused by steric interactions with the silyl substituents. This actually matches up with experiments which indicate that an analogue of TMSPT_P2 is the kinetic product but TMSPT_P3 is the thermodynamic product.

PT_TS3
TMSPT_­TS3
TMSPT_P2	TMSPT_P3
BT_TS2	BT_P2

Figure 1. M06-2x/3-21G* optimized geometries.
(Once again a reminder that clicking on any of these structures will launch JMol and you’ll be able to visualize and manipulate this structure in 3-D.)

The computations involving the Diels-Alder reaction of C₆₀ with either 2a or 2b come to the same conclusion. In both cases, the lowest barrier is for the reaction at ring 2, and the product of the reaction at this same ring is the only one that is endoergonic. The geometries of BT_TS2 and BT_P2 are shown in Figure 1. More importantly, the barrier for the Diels-Alder reaction involving 2a and 2b are at least 6 kcal mol^-1 higher than the barriers for the reaction of 1a and 1b, in complete agreement with experiments that show little reaction involving analogues of 2b with C₆₀, while analogues of 1b are reasonably rapid.

References

(1) Cao, Y.; Liang, Y.; Zhang, L.; Osuna, S.; Hoyt, A.-L. M.; Briseno, A. L.; Houk, K. N. "Why Bistetracenes Are Much Less Reactive Than Pentacenes in Diels–Alder Reactions with Fullerenes," J. Am. Chem. Soc. 2014, 136, 10743-10751, DOI: 10.1021/ja505240e.

Trying to get carbon to bond in unnatural ways seems to be a passion for many organic chemists! Schleyer has been interested in unusual carbon structures for decades and he and Schaefer now report a molecule with a pentacoordinate carbon bound to five other carbon atoms. Their proposed target is pentamethylmethane cation C(CH₃)₅⁺ 1.¹ The optimized geometry of 1, which has C_3h symmetry, at MP2/cc-pVTZ is shown in Figure 1. The bonds from the central carbon to the equatorial carbon are a rather long 1.612 Å, but the bonds to the axial carbon are even longer, namely 1.736 Å. Bader analysis shows five bond critical points, each connecting the central carbon to one of the methyl carbons. Wiberg bond index and MO analysis suggests that the central carbon is tetravalent, with a 2-electron-3-center bond involving the central and axial carbons.

1
TS1	TS2

Figure 1. MP2/cc-pVTZ optimized geometries of 1 and dissociation transition states.

So while 1 is a local energy minimum, it sits in a very shallow well. One computed dissociation path, which passes through TS1 (Figure 1) on its way to 2-methyl-butyl cation and methane has a barrier of only 1.65 kcal mol^-1 (CCSD(T)/CBS + ZPE). A second dissociation pathway goes through TS2 to t-butyl cation and ethane with a barrier of only 1.34 kcal mol^-1. Worse still is that the free energy estimates suggest “spontaneous dissociation … through both pathways”.

Undoubtedly, this will not be the last word on trying to torture a poor carbon atom.

References

(1) McKee, W. C.; Agarwal, J.; Schaefer, H. F.; Schleyer, P. v. R. "Covalent Hypercoordination: Can Carbon Bind Five Methyl Ligands?," Angew. Chem. Int. Ed. 2014, 53, 7875-7878, DOI: 10.1002/anie.201403314.

InChIs

1: InChI=1S/C6H15/c1-6(2,3,4)5/h1-5H3/q+1
InChIKey=GGCBGJZCTGZYFV-UHFFFAOYSA-N

Houk’s theory of torquoselectivity is a great achievement of computational chemistry, as told in Chapter 4.6 of the second edition of my book. Houk, in a collaboration with Krenske and Hsung, now report on an application of torquoselectivity in the formation of a cis-trans-cyclooctadienone intermediate.¹

The proposed reaction is shown in Scheme 1, where the bicyclic compound undergoes a conrotatory ring opening in just one orientation to form the E,E-cyclooctadienone, which can then ring close to product.

Scheme 1.

Houk ran M06-2x//6-311+G(d,p)//B3LYP/6-31G(d) computations on the model system 1, passing over the two torquodistinctive transition states TSEE and TSZZ, and on to produce the two cyclooctadienones 2EE and 2ZZ, respectively. As seen in Figure 1, the barrier through TSEE is favored by 9.8 kcal mol^-1, and leads to the much more favorable cycloocatadienone 2EE.

1 0.0
TSEE 32.3	2EE 9.4
TSZZ 42.1	2ZZ 21.0
TS2 47.5

Figure 1. B3LYP/6-31G(d) optimized structures and relative free energies (kcal mol^-1) at M06-2x//6-311+G(d,p)//B3LYP/6-31G(d).

Ring closure taking TSEE to product goes through TS2 (Figure 1), with a very high barrier, 47.5 kcal mol^-1 above reactant, suggesting that this path is not likely to occur. Instead, they propose that 2EE is first protonated (2EEH⁺) and then cyclizes through TS2H⁺ (Figure 2). This barrier is only 6.2 kcal mol^-1, some 44 kcal mol^-1 lower than the neutral process through TS2.

2EEH+

TS2H+

Figure 2. B3LYP/6-31G(d) optimized structures

References

(1) Wang, X.-N.; Krenske, E. H.; Johnston, R. C.; Houk, K. N.; Hsung, R. P. "Torquoselective Ring Opening of Fused Cyclobutenamides: Evidence for a Cis,Trans-Cyclooctadienone Intermediate," J. Am. Chem. Soc. 2014, 136, 9802-9805, DOI: 10.1021/ja502252t.

Twistane 1 is a more strained isomer of adamantane 2. The structure of 1 is shown in Figure 1.

1

Figure 1. B3LYP/6-31G(d) optimized structure of 1.

Adamantane is the core structure of diamond, which can be made by appending isobutene groups onto adamantane. In an analogous fashion, twistane can be extended in a linear way by appending ethano groups in a 1,4-bridge. Allen, Schreiner, Trauner and co-workers have examined this “polytwistane” using computational techniques.¹ They examined a (CH)₂₃₆ core fragment of polytwistane, with the dangling valences at the edges filled by appending hydrogens, giving a C₂₃₆H₂₄₂ compound. This compound was optimized at B3LYP/6-31G(d) and shown in Figure 2a. (Note that I have zoomed in on the structure, but by activating Jmol – click on the figure – you can view the entire compound.) A fascinating feature of polytwistane is its helical structure, which can be readily seen in Figure 2b. A view down the length of this compound, Figure 2c, displays the opening of this helical cylinder; this is a carbon nanotube with an inner diameter of 2.6 Å.

(a)

(b)

(c)

Figure 2. B3LYP/6-31G(d) structure of the C₂₃₆H₂₄₂ twistane. (a) A zoomed in look at the structure. This structure links to the Jmol applet allowing interactive viewing of the molecule – you should try this! (b) a side view clearly showing its helical nature. (c) A view down the twistane showing the nanotube structure.

Though the molecule looks quite symmetric, each carbon is involved in three C-C bonds, and each is of slightly different length. The authors go through considerable detail about addressing the symmetry and proper helical coordinates of polytwistane. They also estimate a strain energy of about 1.6 kcal mol^-1 per CH unit. This modest strain, they believe, suggests that polytwistanes might be reasonable synthetic targets.

References

(1) Barua, S. R.; Quanz, H.; Olbrich, M.; Schreiner, P. R.; Trauner, D.; Allen, W. D. "Polytwistane," Chem. Eur. J. 2014, 20, 1638-1645, DOI: 10.1002/chem.201303081.

InChIs

1: InChI=1S/C10H16/c1-2-8-6-9-3-4-10(8)5-7(1)9/h7-10H,1-6H2
InChIKey=AEVSQVUUXPSWPL-UHFFFAOYSA-N

2: InChI=1S/C10H16/c1-7-2-9-4-8(1)5-10(3-7)6-9/h7-10H,1-6H2
InChIKey=ORILYTVJVMAKLC-UHFFFAOYSA-N

“How small can a catenane be?” This question is asked by Schaefer, Allinger and colleagues and answered (well, almost answered) using computations.¹ Catenanes are linked rings. The catenanes examined here are two linked saturated hydrocarbon rings, each of the same size. The rings examined have 11 to 18 carbon atoms. The geometries were optimized with D₂ symmetry, where either the closest approach between the two rings are two carbon atoms or the midpoint of two C-C bonds. The former turn out to be lower in energy. Geometries were optimized with MP2, B3LYP, BP86 or M06-2X with the DZP++ basis set. There is little geometric dependence on computational method. The optimized geometry of the catenane with 14 carbons is shown in Figure 1.

Figure 1. Optimized geometry of the 14-carbon catenane. (Be sure to click on this structure to view the molecule in 3-D; you will have to allow Jmol to download and run!)

To cut to the chase, as the rings get smaller they observe a lengthening of the C-C bonds at the intersection. With the 14-carbon catenane they observe a significant increase in the bond length near the intersection, suggesting a dramatic instability. This is also seen in the change in the energy per C as the rings get smaller; a large increase in energy per C is seen at the transition from 14 to 13 carbons. This all points toward the 14-carbon catenane as the smallest one that might be stable.

(I thank Prof. Schaefer and colleagues for providing me with the coordinates of the 14-carbon catenane.)

References

(1) Feng, X.; Gu, J.; Chen, Q.; Lii, J.-H.; Allinger, N. L.; Xie, Y.; Schaefer, H. F. "How Small Can a Catenane Be?," J. Chem. Theor. Comput. 2014, 10, 1511-1517, DOI: 10.1021/ct400926p

While the [2-3]-sigmatropic rearrangement is well known and understood as allowed under the Woodward-Hoffmann rules, [1,2]-sigmatropic are much more rare, perhaps because they are forbidden by the same orbital symmetry arguments. It is perhaps surprising that these two rearrangements may sometimes be found in competition. Singleton has applied many of his tried-and-true techniques, namely, careful normal abundance kinetic isotope effect (KIE) analysis and molecular dynamics computations, to this problem.¹

Reaction 1 takes place exclusively through a [2,3]-rearrangement; the principle evidence is the lack of any crossover reaction. However, the slightly more substituted analogue shown in Reaction 2 gives rise to two products: that obtained from a [2,3]-rearrangement 6 and that obtained from a [1,2]-rearrangement 7.

The KIE for the rearrangement of 2 is large for the carbon breaking the bond with nitrogen, while it is small at the carbons that are forming the new bond. This becomes a metric for judging the transition state obtained with computations. With the computed TS and canonical variational transition state theory (VTST) including small curvature tunneling, the KIE can be computed from a computed structures and frequencies. This imposes a range of reasonable distances for the forming C-C bond of 2.6-2.9 Å – much longer that a typical distance in the TS of similar pericyclic reactions.

Crossover experiments for Reaction 2 are understood in terms of a reaction model whereby some fraction of the reactants undergo a concerted rearrangement to form 6, and 7 is formed by first breaking the C-N bond, forming two radicals, that either recombine right away or form isolated radicals that then collapse to product.

The interesting twist here is that one would expect two different transition states, one for the concerted process 8 and one to cleave the bond 9. Both do exist and are shown in Figure 1. However, VTST predicts that the concerted process should be 25-50 times faster than cleavage, and that does not match up with experiments. Amazingly, molecular dynamics trajectories started from the concerted TS 8 leads to cleavage about 20% of the time using UMO6-2X with a variety of basis sets. Thus, as Singleton has noted many times before, a single TS is crossed that leads to two different products! An argument based on entropy helps explain why the second (cleavage) pathway is viable.

8

9

Figure 1. UMO6-2x/6-31G* optimized structures of TS 8 and 9.

References

(1) Biswas, B.; Collins, S. C.; Singleton, D. A. "Dynamics and a Unified Understanding of Competitive [2,3]- and [1,2]-Sigmatropic Rearrangements Based on a Study of Ammonium Ylides," J. Am. Chem. Soc. 2014, 136, 3740-3743, DOI: 10.1021/ja4128289.

Schreiner provides another beautiful example of the important role that dispersion plays, this time in a biological system.¹ The microbe Candidatus Brocadia Anammoxidans oxidizes ammonia with nitrite. This unusual process must be done anaerobically and without allowing toxic side products, like hydrazine to migrate into the cellular environment. So this cell has a very dense membrane surrounding the enzymes that perform the oxidation. This dense membrane is home to some very unusual lipids, such as 1. These lipids contain the ladderane core, a highly strained unit. Schreiner hypothesized that these ladderane groups might pack very well and very tightly due to dispersion.

1

The geometries of the [2]- through [5]-ladderanes and their dimers were optimized at MP2/aug-cc-pVDZ, and the binding energies corrected for larger basis sets and higher correlation effects. The dimers were oriented in their face-to-face orientation (parallel-displaced dimer, PDD) or edge-to-edge (side-on dimer, SD). Figure 1 shows the optimized structures of the two dimeric forms of [4]-ladderane.

[4]-PDD

[4]-SD

Figure 1. MP2/aug-cc-pVDZ optimized geometries of the dimers of [4]-ladderane in the PDD and SD orientations.

The binding energies of the ladderane dimers, using the extrapolated energies and at B3LYP-D3/6-311+G(d,p), are listed in Table 1. (The performance of the B3LYP-D3 functional is excellent, by the way.)The binding is quite appreciable, greater than 6 kcal mol^-1 for both the [4]- and [5]-ladderanes. Interestingly, these binding energies far exceed the binding energies of similarly long alkanes. So, very long alkyl lipid chains would be needed to duplicate the strong binding. Nature appears to have devised a rather remarkable solution to its cellular isolation problem!

References

(1) Wagner, J. P.; Schreiner, P. R. "Nature Utilizes Unusual High London Dispersion
Interactions for Compact Membranes Composed of Molecular Ladders," J. Chem. Theor. Comput. 2014, 10, 1353-1358, DOI: 10.1021/ct5000499.

InChIs

1: InChI=InChI=1S/C20H30O2/c21-15(22)7-5-3-1-2-4-6-11-10-14-16(11)20-18-13-9-8-12(13)17(18)19(14)20/h11-14,16-20H,1-10H2,(H,21,22)/t11-,12-,13+,14-,16+,17+,18-,19-,20+/m0/s1
InChIKey=ZKKJRZDMLYQUNK-QIPWGTBCSA-N

[2]-ladderane: InChI=1S/C6H10/c1-2-6-4-3-5(1)6/h5-6H,1-4H2/t5-,6+
InChIKey=YZLCEXRVQZNGEK-OLQVQODUSA-N

[3]-ladderane: InChI=1S/C8H12/c1-2-6-5(1)7-3-4-8(6)7/h5-8H,1-4H2/t5-,6+,7+,8-
InChIKey=YTZCZYFFHKYOBJ-SOSBWXJGSA-N

[4]-ladderane: InChI=1S/C10H14/c1-2-6-5(1)9-7-3-4-8(7)10(6)9/h5-10H,1-4H2/t5-,6+,7+,8-,9-,10+
InChIKey=VZHFDSXKIJOCAY-UXAOAXNSSA-N

[5]-ladderane: InChI=1S/C12H16/c1-2-6-5(1)9-10(6)12-8-4-3-7(8)11(9)12/h5-12H,1-4H2/t5-,6+,7-,8+,9+,10-,11-,12+
InChIKey=CWUAAECPDWVJSU-SBBGGFAWSA-N

The importance of dispersion in determining molecular structure, even the structure of a single medium-sized molecule, is now well recognized. This means that quantum methods that do not account for dispersion might give very poor structures.

Grimme¹ takes an interesting new twist towards assessing the geometries produced by computational methods by evaluating the structures based on their rotational constants B₀ obtained from microwave experiments. He uses nine different molecules in his test set, shown in Scheme 1. This yields 25 different rotational constants (only one rotational constant is available from the experiment on triethylamine). He evaluates a number of different computational methods, particularly DFT with and without a dispersion correction (either the D3 or the non-local correction). The fully optimized geometry of each compound with each method is located to then the rotational constants are computed. Since this provides B_e values, he has computed the vibrational correction to each rotational constant for each molecule, in order to get “experimental” B_e values for comparisons.

Scheme 1.

Grimme first examines the basis set effect for vitamin C and aspirin using B3LYP-D3. He concludes that def2-TZVP or lager basis sets are necessary for reliable structures. However, the errors in the rotational constant obtained at B3LYP-D3/6-31G* is at most 1.7%, and even with CBS the error can be as large as 1.1%, so to my eye even this very small basis set may be completely adequate for many purposes.

In terms of the different functionals (using the DZVP basis set), the best results are obtained with the double hybrid B2PLYP-D3 functional where the mean relative deviation is only 0.3%; omitting the dispersion correction only increases the mean error to 0.6%. Common functionals lacking the dispersion correction have mean errors of about 2-3%, but with the correction, the error is appreciably diminished. In fact B3LYP-D3 has a mean error of 0.9% and B3LYP-NL has an error of only 0.6%. In general, the performance follows the Jacob’s Ladder hierarchy.

References

(1) Grimme, S.; Steinmetz, M. "Effects of London dispersion correction in density functional theory on the structures of organic molecules in the gas phase," Phys. Chem. Chem. Phys. 2013, 15, 16031-16042, DOI: 10.1039/C3CP52293H.