Cramer and Truhlar have tested their latest solvation model SM8 against a test set of 17 small, drug-like molecules.¹ Their best result comes with the use of SM8, the MO5-2X functional, the 6-31G(d) basis set and CM4M charge model. This computational model yields a root mean squared error for the solvation free energy of 1.08 kcal mol^-1 across this test set. This is the first time these authors have recommended a particular computational model. Another interesting point is that use of solution-phase optimized geometries instead of gas-phase geometries leads to only marginally improved solvation energies, so that the more cost effective use of gas-phase structures is encouraged.

These authors note in conclusion that further improvement of solvation prediction rests upon “an infusion of new experimental data for molecules characterized by high degrees of functionality (i.e. druglike)”.

References

(1) Chamberlin, A. C.; Cramer, C. J.; Truhlar, D. G., “Performance of SM8 on a Test To Predict Small-Molecule Solvation Free Energies,” J. Phys. Chem. B, 2008, 112, 8651-8655, DOI: 10.1021/jp8028038.

Cramer and Truhlar¹ have published a nice review of their SM8 approach to evaluated solvation energy. Besides a quick summary of the theoretical approach behind the model, they detail a few applications. Principle among these is (a) the very strong performance of SM8 relative to some of the standard approaches in the major QM codes (see my previous blog post), (b) modeling interfaces, and (c) computing pK_a values of organic compounds.

References

(1) Cramer, C. J.; Truhlar, D. G., "A Universal Approach to Solvation Modeling," Acc. Chem. Res. 2008, 41, 760-768, DOI: 10.1021/ar800019z.

Truhlar and Cramer have updated their Solvation Model to SM8.¹ This model allows for any solvent to be utilized (both water and organic solvents) and treats both neutral and charged solutes. While there are some small theoretical changes to the model, the major change is in how the parameters are selected, the number of parameters, and a much more extensive data set is used for the fitting procedure.

Of note is how well this new model works. Table 1 compares the errors in solvation free energies computed using the new SM8 model against some other popular continuum methods. Clearly, SM8 provides much better results. As they point out, what is truly discouraging is the performance of the 3PM model against the continuum methods. 3PM stands for “three-parameter model”, where the solvation energies of all the neutral solute in water is set to their average experimental value (-2.99 kcal mol^-1), and the same for the neutral solutes in organic solvents (-5.38 kcal mol^-1), and for ions (-65.0 kcal mol^-1). The 3PM outperforms most of the continuum methods!

Table 1. Mean unsigned error (kcal mol^-1) for the solvation
free energies computed with different methods.¹

^a274 data points. ^b666 data points spread among 16 solvents. ^c332 data points spread among acetonitrile, water, DMSO, and methanol. ^dUsing mPW1PW/6-31G(d). ^eUsing mPW1PW/6-31G(d) and the UA0 atomic radii in Gaussian. ^fUsing mPW1PW/6-31G(d) and the UAHF atomic radii in Gaussian. ^gUsing B3LYP/6-31G(d) and conductor-PCM in GAMESS. ^hUsing B3LYP/6-31G(d) and the PB method in Jaguar.

References

(1) Marenich, A. V.; Olson, R. M.; Kelly, C. P.; Cramer, C. J.; Truhlar, D. G., "Self-Consistent Reaction Field Model for Aqueous and Nonaqueous Solutions Based on Accurate Polarized Partial Charges," J. Chem. Theory Comput., 2007, 3, 2011-2033. DOI: 10.1021/ct7001418.

The Highlights article¹ in a recent issue of Angewandte Chemie Intermational Edition concerns the induced chirality of an achiral solvent by a chiral solute determining the overall optical activity. I blogged on this in my last post. This Highlights article stressed (as I did) the novelty of this effect and the need for further experiments and computation. I am sure that more will come in this exciting area.

It is also interesting to me that Angewandte would feature in this way one of its own articles. Isn’t the fact that it was accepted and then published in the journal sufficient stamp of its novelty and importance? Can anyone say “nepotism”?

References

(1) Neugebauer, J., “Induced Chirality in Achiral Media – How Theory Unravels Mysterious Solvent Effects,” Angew. Chem. Int. Ed., 2007, 46, 7738-7740, DOI: 10.1002/anie.200702858.

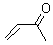
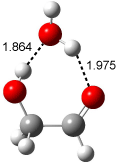
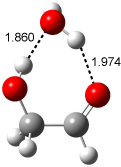
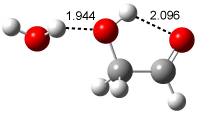
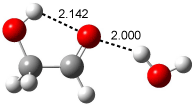
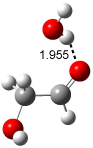
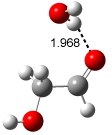
Bertran and Wipf have examined the role of solvent organization about a chiral molecule in producing the optical activity.¹ They generated 1000 configurations of benzene arrayed about methyloxirane from a Monte Carlo simulation. Each configuration was then constructed by keeping every benzene molecules within 0.5 nm from the center-of-mass of methyloxirane, usually 8-10 solvent molecules. The optical rotation was then computed at four wavelengths using TDDFT at BP86/SVP. (The authors note that though the Gaussian group recommends B3LYP/aug-ccpVDZ,^2-4 using the non-hybrid functional allows the use of resolution-of–the-identity⁵ techniques that make the computations about six orders of magnitude faster – of critical importance given the size of the clusters and the sheer number of them!) Optical rotation is then obtained by averaging over the ensemble.

The computed optical rotations disagree with the experiment by about 50% in magnitude but have the correct sign across the four different wavelengths. Use of the COSMO model (implicit solvent) provides the wrong sign at short wavelengths. But perhaps most interesting is that the computed optical activity of the solvent molecules in the configuration about the solute, but without including methyloxirane, is nearly identical to that of the whole cluster! In other words, the optical activity is due to the dissymmetric distribution of the solvent molecules about the chiral molecule, not the chiral molecule itself! It is the imprint of the chiral molecule on the solvent ordering that accounts for nearly all of the optical activity.

References

(1) Mukhopadhyay, P.; Zuber, G.; Wipf, P.; Beratan, D. N., "Contribution of a Solute’s
Chiral Solvent Imprint to Optical Rotation," Angew. Chem. Int. Ed. 2007,
46, 6450-6452, DOI: 10.1002/anie.200702273

(2) Stephens, P. J.; McCann, D. M.; Cheeseman, J. R.; Frisch, M. J., "Determination of
absolute configurations of chiral molecules using ab initio time-dependent Density Functional Theory calculations of optical rotation: How reliable are absolute configurations obtained for molecules with small rotations?," Chirality 2005, 17, S52-S64, DOI: 10.1002/chir.20109.

(3) Stephens, P. J.; Devlin, F. J.; Cheeseman, J. R.; Frisch, M. J., "Calculation of Optical Rotation Using Density Functional Theory," J. Phys. Chem. A 2001, 105, 5356-5371, DOI: 10.1021/jp0105138.

(4) Stephens, P. J.; McCann, D. M.; Devlin, F. J.; Flood, T. C.; Butkus, E.; Stoncius,
S.; Cheeseman, J. R., "Determination of Molecular Structure Using Vibrational Circular Dichroism Spectroscopy: The Keto-lactone Product of Baeyer-Villiger Oxidation of (+)-(1R,5S)-Bicyclo[3.3.1]nonane-2,7-dione," J. Org. Chem. 2005, 70, 3903-3913, DOI: 10.1021/jo047906y.

(5) Eichkorn, K.; Treutler, O.; Ohm, H.; Haser, M.; Ahlrichs, R., "Auxiliary Basis Sets to Approximate Coulomb Potentials," Chem. Phys. Lett. 1995, 240, 283-289, DOI: 10.1016/0009-2614(95)00621-A.

Jorgensen reports an enhanced QM/MM and ab initio study of the rate enhancement of Diels-Alder reactions in various solvents.¹ This study extends earlier studies that he and others have done, many of which are discussed in Chapter 6.2 of the book. In this study, he reports QM/MM computations using the PDDG/PM3 method for the QM component, and MP2 computations incorporating CPCM to account for bulk solvent effects.

The major advance in methodology in this paper is performing a two-dimensional potential of mean force analysis where these two dimensions correspond to the forming C-C distances. In addition, computations were done for water, methanol, acetonitrile and hexane as solvents. Highlights of the results are listed in Table 1.

Table 1. Computed bond asynchronicity^a and activation energy^b (kcal/mol) for the Diels-Alder reaction with cyclopentadiene.

The semi-empirical method underestimates the asynchronicity of these gas-phase Diels-Alder TSs. However, with inclusion of the solvent, the computations do indicate a growing asynchronicity with solvent polarity, This is associated with the ability of the solvent, especially protic solvents, to preferentially hydrogen bond to the carbonyl in the TS.

In terms of energetics, in must first be pointed out that the computations dramatically overestimate the activation barriers. However, the relative trends are reproduced: the barrier increases from water to methanol to acetonitrile to hexane. Jorgensen also computed the activation barriers at MP2/6-311+G(2d,p) with CPCM using the CBS=QB3 gas phase geometries. Some of these results are listed in Table 2. The results for water are in outstanding agreement with experiment. However, the results for the other solvents are poor, underestimating the increase in barrier in moving to the more polar solvent.

Table 2. MP2/6-311+G(2d,p)/CPCM values for ΔG^‡ (kcal/mol).

Bottom line, the conclusions of this study are in agreement with the earlier studies, namely that the hydrophobic effect (better may be the enforced hydrophobic interaction) and greater hydrogen bonding in the TS (both more and stronger hydrogen bonds) account for the rate acceleration of the Diels-Alder reaction in water.

References

(1) Acevedo, O.; Jorgensen, W. L., "Understanding Rate Accelerations for Diels-Alder Reactions in Solution Using Enhanced QM/MM Methodology," J. Chem. Theory Comput. 2007, 3, 1412-1419, DOI: 10.1021/ct700078b.

Monohydrated Glycolaldehyde (2-hydroxyethanal)

In Chapter 6.3.1 we discussed the conformation energy profile of solvated ethylene glycol and glycerol. The conformational preference is determined by the two competing hydrogen bonding interactions: intramolecular hydrogen bonding versus hydrogen bonding to the water molecules. For both glycerol and ethylene glycol, the lowest energy solvated structures retain the maximal number of internal hydrogen bonds possible.

The conformational space of glycoladehyde 1 exhibits four local minima. ¹ The lowest energy structure possesses an internal hydrogen bond, 1-CC (Figure 1). The other conformers are at least 3 kcal mol^-1 higher in energy. Will this internal hydrogen bond persist when 1 is hydrated?

1-CC (0.0) xyz file	1-TT (3.06) xyz file
1-TG (3.33) xyz file	1-CT (4.84) xyz file

Figure 1. Optimized geometries of the conformers of 1 at MP2/aug-cc-pVTZ. ¹ The letters C, T, and G indicate cis¸ trans, or gauche around the C-C and C-O bonds, in that order. Relative energies in kcal mol^-1.

A recent computational (B3LYP/6-311++G(2df,p)) and experimental study examined the structure of monohydrated glycoladehyde.² Optimization of the monohydrated cluster of 1 indicated that the lowest energy structures all have the glycolaldehyde fragment in the CC conformation (see Figure 2). The lowest energy cluster not in the CC arrangement is 1-TG-w, and it lies 2.86 kcal mol^-1 above the lowest monohydrate, 1-CC-w1.

The lowest energy monohydrate (1-CC-w1) does not maintain the internal hydrogen bond of 1-CC. Rather, the water molecule inserts into this hydrogen bond, such that it donates a hydrogen to the carbonyl oxygen, and accepts the hydrogen from the hydroxyl group. The other conformations provide no opportunity for forming two hydrogen bonds with a water molecule, and so their hydrates are higher in energy. The microwave FT spectrum² of the monohydrate of 1 is interpreted as a dynamic interconversion of the two lowest energy complexes, 1-CC-w1 and 1-CC-w2.

1-CC-w1 (0.0) xyz file	1-CC-w2 (0.51) xyz file
1-CC-w3 (0.96) xyz file	1-CC-w4 (1.39) xyz file
1-TG-w (2.86) xyz file	1-TT-w (3.71) xyz file
1-CT-w (5.98) xyz file

Figure 2. Optimized geometries (B3LYP/6-311++G(2df,p)) of the monohydrated glycolaldehyde structures.² All distances in Å and relative energies (G3MP2B3) in kcal mol^-1.

References

(1) Ratajczyk, T.; Pecul, M.; Sadlej, J.; Helgaker, T., “Potential Energy and Spin-Spin Coupling Constants Surface of Glycolaldehyde,” J. Phys. Chem. A 2004, 108, 2758-2769, DOI: 10.1021/jp0375315

(2) Aviles-Moreno, J. R.; Demaison, J.; Huet, T. R., “Conformational Flexibility in Hydrated Sugars: the Glycolaldehyde-Water Complex,” J. Am. Chem. Soc. 2006, 128, 10467-10473, DOI: 10.1021/ja062312t