Optical activity is a major tool for identifying enantiomers. With recent developments in computational techniques, it is hoped that experiments combined with computations will be a powerful tool for determining absolute configuration. The recent work of Lahiri, et al. demonstrates the scope of theoretical work that is still needed to really make this approach broadly applicable.¹

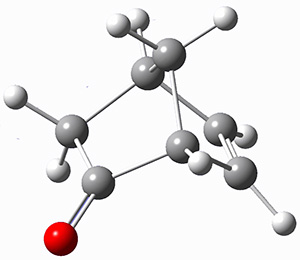
They prepared (1R,4R)-norbornenone 1 and measured its optical rotation in the gas phase and in dilute solutions of acetonitrile and cyclohexane. The specific rotations at three different wavelengths are listed in Table 1. Of first note is that though there is some small differences in solution, as expected, there really is substantial differences between the gas- and solution phases. Thus cautionary point 1: be very careful of comparing solution phase experimental optical activity with computed gas phase predictions.

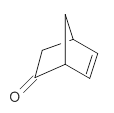
1

Table 1. Experimental and computed specific rotation of 1.

For the computations, the geometry of 1 was optimized at B3LYP/aug-cc-pVTZ (see Figure 1. The OR was computed at B3LYP with different basis sets, finding that the difference in the predicted specific rotation at 598.3nm differs only quite little (90.6 deg dm^-1 (g/mL)^-1) between the computations using aug-cc-pVTZ and aug-cc-pVQZ) suggesting that the basis set limit has been reached. The gas –phase computed values at B3LYP and CCSD are also shown in Table 1. Though these computations do get the correct sign of the rotation, they are appreciably off of the experimental values, and the percent error varies with wavelength. Cautionary point 2: it is not obvious what is the appropriate computational method to compute OR, and beware of values that seem reasonable at one wavelength – this does not predict a good agreement at a different wavelength.

Figure 1. Optimized geometry of 1 at B3LYP/aug-cc-pVTZ.

Lastly, computed solution values of the OR were performed with PCM and B3LYP. These values are given in Table 1. Again the agreement is poor. So cautionary point 3: computed (PCM) solution OR
may be in quite poor agreement with experiment.

Often the culprit to poor agreement between computed and experimental OR is attributed to omitted vibrational effects, but in this case, because 1 is so rigid, one might not expect too much error to be caused by the effects of vibrations. So the overall result – we need considerable work towards addressing how to accurately compute optical activity!

References

(1) Lahiri, P.; Wiberg, K. B.; Vaccaro, P. H.; Caricato, M.; Crawford, T. D. "Large Solvation Effect in the Optical Rotatory Dispersion of Norbornenone," Angew. Chem. Int. Ed. 2014, 53, 1386-1389, DOI: 10.1002/anie.201306339.

InChIs

1: InChI=1S/C7H8O/c8-7-4-5-1-2-6(7)3-5/h1-2,5-6H,3-4H2/t5-,6+/m1/s1
InChIKey=HUQXEIFQYCVOPD-RITPCOANSA-N

Computing the optical rotation of simple organic molecules can be a real challenge. One of the classic problems is methyloxirane. DFT typically gets the wrong sign, let alone the wrong value. Cappelli and Barone¹ have developed a QM/MM procedure where methyloxirane is treated with DFT (B3LYP/aug-cc-pVDZ or CAM-B3LYP/aubg-cc-pVDZ). Then 2000 arrangements of water about methyloxirane were obtained from an MD simulation. For each of these configurations, a supermolecule containing methyloxirane and all water molecules with 16 Å was identified. The waters of the supermolecule were treated as a polarized force field. This supermolecule is embedded into bulk water employing a conductor-polarizable continuum model (C-PCM). Lastly, inclusion of vibrational effects, and averaging over the 2000 configurations, gives a predicted optical rotation at 589 nm that is of the correct sign (which is not accomplished with a gas phase or simple PCM computation) and is within 10% of the correct value. The full experimental ORD spectrum is also quite nicely matched using this theoretical approach.

References

(1) Lipparini, F.; Egidi, F.; Cappelli, C.; Barone, V. "The Optical Rotation of Methyloxirane in Aqueous Solution: A Never Ending Story?," J. Chem. Theor. Comput. 2013, 9, 1880-1884, DOI: 10.1021/ct400061z.

InChIs

(R)-Methyloxirane:
InChI=1S/C3H6O/c1-3-2-4-3/h3H,2H2,1H3/t3-/m1/s1
InChIKey=GOOHAUXETOMSMM-GSVOUGTGSA-N

Conformational analysis is one of the tasks that computation chemistry is typically quite adept at and computational chemistry is frequently employed for this purpose. Thus, benchmarking methods for their ability to predict accurate conformation energies is quite important. Martin has done this for alkanes¹ (see this post), and now he has looked at a molecule that contains weak intramolecular hydrogen bonds. He examined 52 conformations of melatonin 1.² The structures of the two lowest energy conformations are shown in Figure 1.

1

1a

1b

Figure 1. Structures of the two lowest energy conformers of 1 at SCS-MP2/cc-pVTZ.

The benchmark (i.e. accurate) relative energies of these conformers were obtained at MP2-F12/cc-pVTZ-F12 with a correction for the role of triples: (ECCSD(T)/cc-pVTZ)-E(MP2/cc-pVTZ)). The energies of the conformers were computed with a broad variety of basis sets and quantum methodologies. The root mean square deviation from the benchmark energies is used as a measure of the utility of these alternate methodologies. Of particular note is that HF predicts the wrong ordering of the two lowest energy isomers, as do some DFT methods that use small basis sets and do not incorporate dispersion.

In fact, other than the M06 family or double hybrid functionals, all of the functionals examined here (PBE. BLYP, PBE0, B3LYP, TPSS0 and TPSS) have RMSD values greater than 1 kcal mol^-1. However, inclusion of a dispersion correction, Grimme’s D2 or D3 variety or the Vydrov-van Voorhis (VV10) non-local correction (see this post for a review of dispersion corrections), reduces the error substantially. Among the best performing functionals are B2GP-PLYP-D3, TPSS0-D3, DSD-BLYP and M06-2x. They also find the MP2.5 method to be a practical ab initio alternative. One decidedly unfortunate result is that large basis sets are needed; DZ basis sets are simply unacceptable, and truly accurate performance requires a QZ basis set.

References

(1) Gruzman, D.; Karton, A.; Martin, J. M. L. "Performance of Ab Initio and Density Functional Methods for Conformational Equilibria of CnH2n+2 Alkane Isomers (n = 4-8)," J. Phys. Chem. A 2009, 113, 11974–11983, DOI: 10.1021/jp903640h.

(2) Fogueri, U. R.; Kozuch, S.; Karton, A.; Martin, J. M. L. "The Melatonin Conformer Space: Benchmark and Assessment of Wave Function and DFT Methods for a Paradigmatic Biological and
Pharmacological Molecule," J. Phys. Chem. A 2013, 117, 2269-2277, DOI: 10.1021/jp312644t.

InChIs

1: InChI=1S/C13H16N2O2/c1-9(16)14-6-5-10-8-15-13-4-3-11(17-2)7-12(10)13/h3-4,7-8,15H,5-6H2,1-2H3,(H,14,16)
InChIKey=DRLFMBDRBRZALE-UHFFFAOYSA-N

Truhlar has made a comparison of binding energies and relative energies of five (H₂O)₁₆ clusters.¹ While technically not organic chemistry, this paper is of interest to the readership of this blog as it compares a very large collection of density functionals on a problem that involves extensive hydrogen bonding, a problem of interest to computational organic chemists.

The CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVTZ energies of clusters 1-5 (shown in Figure 1) were obtained by Yoo.² These clusters are notable not just for their size but also that they involve multiple water molecules involved in four hydrogen bonds. Truhlar has used these geometries to compute the energies using 73 different density functionals with the jun-cc-pVTZ basis set (see this post for a definition of the ‘jun’ basis sets). Binding energies (relative to 16 isolated water molecules) were computed along with the 10 relative energies amongst the 5 different clusters. Combining the results of both types of energies, Truhlar finds that the best overall performance relative to CCSD(T) is obtained with ωB97X-D, a hybrid GGA method with a dispersion correction. The next two best performing functionals are LC-ωPBE-D3 and M05-2x. The best non-hybrid performance is with revPBE-D3 and B97-D.

1 (0.0)	2 (0.25)
3 (0.42)	4 (0.51)
5 (0.54)

Figure 1. MP2/aug-cc-pVTZ optimized geometries and relative CCSD(T) energies (kcal mol^-1) of (water)₁₆ clusters 1-5. (Don’t forget to click on any of these molecules above to launch Jmol to interactively view the 3-D structure. This feature is true for all molecular structures displayed in all of my blog posts.)

While this study can help guide selection of a functional, two words of caution. First, Truhlar notes that the best performing methods for the five (H₂O)₁₆ clusters do not do a particularly great job in getting the binding and relative energies of water hexamers, suggesting that no single functional really stands out as best. Second, a better study would also involve geometry optimization using that particular functional. Since this was not done, one can garner little here about what method might be best for use in a typical study where a geometry optimization must also be carried out.

References

(1) Leverentz, H. R.; Qi, H. W.; Truhlar, D. G. "Assessing the Accuracy of Density
Functional and Semiempirical Wave Function Methods for Water Nanoparticles: Comparing Binding and Relative Energies of (H₂O)₁₆ and (H₂O)₁₇ to CCSD(T) Results," J. Chem. Theor. Comput. 2013, ASAP, DOI: 10.1021/ct300848z.

(2) Yoo, S.; Aprà, E.; Zeng, X. C.; Xantheas, S. S. "High-Level Ab Initio Electronic Structure Calculations of Water Clusters (H₂O)₁₆ and (H₂O)₁₇: A New Global Minimum for (H₂O)₁₆," J. Phys. Chem. Lett. 2010, 1, 3122-3127, DOI: 10.1021/jz101245s.

This is a short post mainly to bring to the reader’s attention a couple of recent JCTC papers.

The first is a benchmark study by Hujo and Grimme of the geometries produced by DFT computations that are corrected for dispersion.¹ They use the S22 and S66 test sets that span a range of compounds expressing weak interactions. Of particular note is that the B3LYP-D3 method provided the best geometries, suggesting that this much (and justly) maligned functional can be significantly improved with just the simple D3 fix.

The second paper entails the description of Truhlar and Cramer’s latest iteration on their solvation model, namely SM12.² The main change here is the use of Hirshfeld-based charges, which comprise their Charge Model 5 (CM5). The training set used to obtain the needed parameters is much larger than with previous versions and allows for treating a very broad set of solvents. Performance of the model is excellent.

References

(1) Hujo, W.; Grimme, S. "Performance of Non-Local and Atom-Pairwise Dispersion Corrections to DFT for Structural Parameters of Molecules with Noncovalent Interactions," J. Chem. Theor. Comput. 2013, 9, 308-315, DOI: 10.1021/ct300813c

(2) Marenich, A. V.; Cramer, C. J.; Truhlar, D. G. "Generalized Born Solvation Model SM12," J. Chem. Theor. Comput. 2013, 9, 609-620, DOI: 10.1021/ct300900e

A comprehensive evaluation of how different computational methods perform in predicting the energies of monosaccharides comes to some very interesting conclusions. Sameera and Pantazis¹ have examined the eight different aldohexoses (allose, alltrose, glucose, mannose, gulose, idose, galactose and talose), specifically looking at different rotomers of the hydroxymethyl group, α- vs. β-anomers, pyranose vs. furanose isomers, ring conformations (¹C₄ vs skew boat forms), and ring vs. open chain isomers. In total, 58 different structures were examined. The benchmark computations are CCSD(T)/CBS single point energies using the SCS-MP2/def2-TZVPP optimized geometries. The RMS deviation from these benchmark energies for some of the many different methods examined are listed in Table 1.

Table 1. Average RMS errors (kJ mol^-1) of the 58 different monosaccharide structures for
different computational methods.

Perhaps the most interesting take-home message is that CEPA, MP2, the double hybrid methods and M06-2x all do a very good job at evaluating the energies of the carbohydrates. Given the significant computational advantage of M06-2x over these other methods, this seems to be the functional of choice! The poorer performance of the DFT methods over the ab initio methods is primarily in the relative energies of the open-chain isomers, where errors can be on the order of 10-20 kJ mol^-1 with most of the functionals; even the best overall methods (M06-2x and the double hybrids) have errors in the relative energies of the open-chain isomers of 7 kJ mol^-1. This might be an area of further functional development to probe better treatment of the open-chain aldehydes vs. the ring hemiacetals.

References

(1) Sameera, W. M. C.; Pantazis, D. A. "A Hierarchy of Methods for the Energetically Accurate Modeling of Isomerism in Monosaccharides," J. Chem. Theory Comput. 2012, 8, 2630-2645, DOI:10.1021/ct3002305

I just returned from the Southwest Theoretical Chemistry Conference held at Texas A&M University. My thanks again to Steven Wheeler for the invitation to speak at the meeting and for putting together a very fine program and conference.

Among the many interesting talks was one by Sebastian Kozuch who reported on an interesting double hybrid methodology.^1,2 Working with Jan Martin, they defined a procedure that Kozuch referred to as “putting Stefan Grimme into a blender”. They extend the double hybrid concept first suggested by Grimme that adds on an MP2-like correction functional. Kozuch and Martin substitute a spin-component scaled MP2 (SCS-MP2) model for the original MP2 correction. SCS-MP2 was also proposed by Grimme. Lastly, they add on a dispersion correction, an idea championed by Grimme too. The exchange-correlation term is defined as

E_XC = c_XE_X ^DFT + (1 – c_x)E_x^HF + c_CE_C^DFT + c_OE_O^MP2 + c_SE_S^MP2 + s₆E_D

where c_X is the coefficient for the amount of DFT exchange, c_C the amount of DFT correlation, c_C and c_S the amount of opposite- and same-spin MP2, and s₆ the amount of dispersion. They name this procedure DSD-DFT for Dispersion corrected, Spin-component scaled Double hybrid DFT.

In their second paper on this subject, they propose the use of the PBEP86 functional for the DFT components.² Benchmarking against a variety of standard databases, including kinetic data, thermodynamic data, along with inorganic and weakly interacting systems, this method delivers the lowest mean error among a small set of functionals. Kozuch reported at the conference on a number of other combinations and should have a publication soon suggesting an even better method. Importantly, these DSD-DFT computations can be run with most major quantum codes including Orca, Molpro, Q-Chem and Gaussian (with a series of IOP specifications).

While double hybrid methods don’t have quite the performance capabilities of regular DFT, density fitting procedures offer the possibility of a significant reduction in computational time. These DSD-DFT methods are certainly worthy of fuller explorations.

References

(1) Kozuch, S.; Gruzman, D.; Martin, J. M. L. "DSD-BLYP: A General Purpose Double Hybrid Density Functional Including Spin Component Scaling and Dispersion Correction," J. Phys. Chem. C, 2010, 114, 20801-20808,
DOI: 10.1021/jp1070852

(2) Kozuch, S.; Martin, J. M. L. "DSD-PBEP86: in search of the best double-hybrid DFT with spin-component scaled MP2 and dispersion corrections," Phys. Chem. Chem. Phys. 2011, 13, 20104-20107, DOI: 10.1039/C1CP22592H

For those of you interested in learning about dispersion corrections for density functional theory, I recommend Grimme’s latest review article.¹ He discusses four different approaches to dealing with dispersion: (a) vdW-DF methods whereby a non-local dispersion term is included explicitly in the functional, (b) parameterized functional which account for some dispersion (like the M06-2x functional), (c) semiclassical corrections, labeled typically as DFT-D, which add an atom-pair term that typically has an r^-6 form, and (d) one-electron corrections.

The heart of the review is the comparison of the effect of including dispersion on thermochemistry. Grimme nicely points out that reaction energies and activation barriers typically are predicted with errors of 6-8 kcal mol^-1 with conventional DFT, and these errors are reduced by up to 1.5 kcal mol^-1 with the inclusion fo the “-D3” correction. Even double hybrid methods, whose mean errors are much smaller (about 3 kcal mol^-1), can be improved by over 0.5 kcal mol^-1 with the inclusion of the “-D3” correction. The same is also true for conformational energies.

Since the added expense of including the “-D3” correction is small, there is really no good reason for not including it routinely in all types of computations.

(As an aside, the article cited here is available for free through the end of this year. This new journal WIREs Computational Molecular Science has many review articles that will be of interest to readers of this blog.)

References

(1) Grimme, S., "Density functional theory with London dispersion corrections," WIREs Comput. Mol. Sci., 2011, 1, 211-228, DOI: 10.1002/wcms.30

The much publicized failure of common DFT methods to accurately describe alkane isomer energy and bond separation reactions (which I have blogged about many times) has recently been attributed to long-range exchange¹ (see this post) or simply just DFT exchange² (see this post). Grimme now responds by emphatically claiming that it is a failure in accounting for medium-range electron correlation.³

First, Grimme notes that the bond separation energy for linear alkanes (as defined in
Reaction 1) is underestimated by HF, and slightly overestimated by MP2, but SCS-MP2 provides energy in nice agreement with CCSD(T)/CBS energies. Since MP2 adds in coulomb correlation to the HF energy (which treats exchange exactly within a one determinant wavefunction), the traditional wavefunction approach strongly suggests a correlation error.

CH₃(CH₂)_mCH₃ + mCH₄ → (m+1)CH₃CH₃        Reaction 1

Next, bond separation energies computed with PBE and BLYP (which lack exact exchange), PBE0 (which has 25% non-local exchange) and BHLYP (which has 50% non-local exchange) are all similar and systematically too small. So, exchange cannot be the culprit. It must be correlation.

He also makes two other interesting points. First, inclusion of a long-range correction – his recently proposed D3 method⁴ – significantly improves results, but the bond separation energies are still underestimated. It is only with the double-hybrid functional B2PLYP and B2GPPLYP that very good bond separation energies are obtained. And these methods do address the medium-range correlation issue. Lastly, Grimme notes that use of zero-point vibrational energy corrected values or enthalpies based on a single conformation are problematic, especially as the alkanes become large. Anharmonic corrections become critical as does inclusion of multiple conformations with increasing size of the molecules.

References

(1) Song, J.-W.; Tsuneda, T.; Sato, T.; Hirao, K., "Calculations of Alkane Energies Using Long-Range Corrected DFT Combined with Intramolecular van der Waals Correlation," Org. Lett., 2010, 12, 1440–1443, DOI: 10.1021/ol100082z

(2) Brittain, D. R. B.; Lin, C. Y.; Gilbert, A. T. B.; Izgorodina, E. I.; Gill, P. M. W.; Coote, M. L., "The role of exchange in systematic DFT errors for some organic reactions," Phys. Chem. Chem. Phys., 2009, DOI: 10.1039/b818412g.

(3) Grimme, S., "n-Alkane Isodesmic Reaction Energy Errors in Density Functional Theory Are Due to Electron Correlation Effects," Org. Lett. 2010, 12, 4670–4673, DOI: 10.1021/ol1016417

(4) Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H., "A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu," J. Chem. Phys., 2010, 132, 154104, DOI: 10.1063/1.3382344.

Computing anions have long been understood to offer interesting challenges. For example, anions require diffuse functions for reasonable description. Jensen¹ has now investigated the electron affinity of atoms and small molecules with three DFT methods: BHHLYP having 50% HF and 50% Becke exchange, B3LYP having 20% HF and 80% Becke exchange and BLYP with 100% Becke exchange. The result is that all three express varying degrees of electron loss from the atom or molecule in the anion. Thus the anionic species really possess only fractional anionic charge.

In cation-anion pairs or in large species that have strong electron acceptors and donors (say a protein), this electron loss manifests itself in less ionic character than what should actually be present. In other words density is erroneously moved off of the anionic center and transferred to the cationic center.

This error is due to poor description of the long-range exchange. Including the LC correction does eliminate the problem, and so one should be very careful in using DFT for anions.

References

(1) Jensen, F., "Describing Anions by Density Functional Theory: Fractional Electron Affinity," J. Chem. Theory Comput., 2010, 6, 2726-2735, DOI: 10.1021/ct1003324