Computed optical activity was utilized in establishing the absolute configuration of the [3,3]paracyclophane 1.¹ The helical twist of this molecule makes it chiral.

The specific rotation of (-)-1 was measured to be -123 ° [dm (g/cm³) ^-1]. Seven different conformations of R–1 were optimized, having either D₂, C₂, or C₁ symmetry, at B3LYP/TZVP. The two lowest energy conformers (at B3LYP/6-31G(d) – the authors did not supply coordinates in their supporting materials!) are shown in Figure 1.

1a (0.0)

1b (0.49)

Figure 1. B3LYP/6-31G(d) optimized structures and relative energy (kcal mol^-1 of the two lowest energy conformers of 1.

The TDDFT computed value for [α]_D for the lowest energy conformer is -171.7 ° [dm (g/cm³)^-1]. In fact, the range of [α]_D for seven conformers is -124.4 to -221.8. These values are consistent with the experimental observation in both sign and magnitude. The computed CD spectrum of the seven R–1 conformations are similar to the experimental spectra of (-)-1. Thus, one can conclude that the two enantiomers are R-(-)-1 and S-(+)-1.

References

(1) Muranaka, A.; Shibahara, M.; Watanabe, M.; Matsumoto, T.; Shinmyozu, T.; Kobayashi, N., "Optical Resolution, Absolute Configuration, and Chiroptical Properties of Three-Layered [3.3]Paracyclophane(1)," J. Org. Chem., 2008, 73, 9125-9128, DOI: 10.1021/jo801441h

InChIs

1: InChI=1/C31H38/c1-3-7-28-22-30-12-6-10-27-20-18-26(19-21-27)9-5-11-29(28)23-31(30)13-4-8-25-16-14-24(2)15-17-25/h14-23H,3-13H2,1-2H3
InChIKey=GFTKQZANYFICNS-UHFFFAOYAN

A real tour-de-force experimental and computational study of the ORD of 2,3-hexadiene 1 has been produced through the combined efforts of Wiberg, Jorgensen, Crawford, Cheeseman and colleagues.¹ You might not expect a simple compound like 1 to display anything particularly unusual, but you’d be wrong!

2,3-hexadiene exists as three conformations, shown in Figure 1. The cis conformers is the lowest energy form, but the other two are only 0.2 kcal mol^-1 higher in energy, meaning that all three will have significant mol fractions at 0 °C, as listed in Figure 1. The optical rotation for each conformer was determined using B3LYP/aug-cc-pVDZ and CCSD/aug-ccpVDZ. While there is some disagreement in the values determined by the two methods, what is most interesting is that large dependence of [α]_D on the conformation – see Table 1!

cis 0.0 (0.441)

gauche120 0.269 (0.280)

gauche240 0.272 (0.279)

Figure 1. CCSDT optimized geometries of 1, their relative energies (kcal mol^-1) and, in parenthesis, their mol fractions at 0 °C.¹

Table 1. Calculated [α]_D for 1.

^aUsing the aug-ccpVDZ basis set. ^aBoltzman averaged based on the populations shown in Figure 1.

The ORD spectrum of 1 was taken for neat liquid and in the gas phase. The computed and experimental optical rotations are listed in Table 2. Two interesting points can be made from this data. First, the optical activity of 1 is strongly affected by phase. Second, the computed optical rotations, especially the CCSD values, are in fairly good agreement with the gas-phase experimental values.

Table 2. Boltzmann-weighted computed and experimental optical rotations of 1.

A hypothesis to account for the large difference in the gas- and liquid-phase ORD for 1 is that the conformational distribution changes with the phase. The gas and liquid-phase ORD of 2,3-pentadiene shows the same strong phase dependence, even though this compound exists as only one conformer.

Next, a Monte Carlo simulation of gas- and liquid-phase 1 was performed to assess the conformational distributions. Though the range of dihedral angle distributions span about 60°, the population distribution is nearly identical in the two phases – there is no medium-dependence on the conformation distribution, and so this cannot explain the difference in the gas and liquid ORDs.

The authors also tested for the vibrational dependence on the optical rotation. While there is a small correction due to vibrations, it is not enough to account for the differences due to the medium. The origin of this effect remains unexplained.

References

(1) Wiberg, K. B.; Wang, Y. g.; Wilson, S. M.; Vaccaro, P. H.; Jorgensen, W. L.; Crawford, T. D.; Abrams, M. L.; Cheeseman, J. R.; Luderer, M., "Optical Rotatory Dispersion of 2,3-Hexadiene and 2,3-Pentadiene," J. Phys. Chem. A, 2008, DOI: 10.1021/jp076572o.

InChIs

1: InChI=1/C6H10/c1-3-5-6-4-2/h3,6H,4H2,1-2H3/t5-/m1/s1 InChIKey=DPUXQWOMYBMHRN-RXMQYKEDBA

I discuss computational prediction of optical rotation in Chapter 1.6.3. I want to address a new protocol for determining absolute configuration using computed spectral properties and a recent review of state-of-the-art computational methods for predicting optical activity.

Stephens and the Gaussian personnel developed the techniques for computing optical rotation, electronic circular dichroism (ECD) and vibrational circular dichroism (VCD).^1-4 Over the past year, Stephens has implemented a protocol for computing these properties in order to determine the absolute configuration of a chiral molecule.^5-7 The first application was to the structures of the related sesquiterpenes 1-4.⁵ A Monte Carlo conformational search is first carried out using MMFF94, and all low energy conformers are reoptimized at B3LYP/6-31G*. Restricted searches by varying some dihedral angles are also sometimes used to insure that all reasonable low-energy conformations have been identified. Then, using these optimized geometries,specific rotations and ECD are computed at TDDFT/B3LYP/aug-cc-pVDZ, and IR and VCCD spectra computed at B3LYP and B3PW91 with the TZ2P basis set.

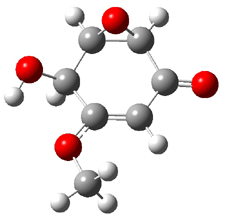
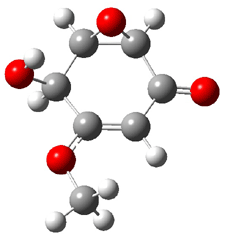
The computed and experimental optical rotations at the sodium D line for 1-4 are listed in Table 1. The computed values of [α]_D for 1 as the 1R,2R,5S,8R,11R isomer (as shown above) is in reasonable agreement with the experimental value – with error similar to those I describe in the book. This is in agreement with the assigned absolute configuration of naturally occurring 1. While the core structures of 2-4 are likely to be identical to 1 assuming similar biosynthesis, their absolute configurations have not been determined. The computed optical rotation for 3 and 4 are again in reasonable agreement with experiment, but for 2 the errors are large for either enantiomer. This is where ECD and VCD are valuable. The computed ECD and VCD spectra of 1 are in extraordinary agreement with the experimental spectra, confirming the assigned absolute configuration. Stephens reports the ECD and VCD spectra of 2-4 and finds that they all have identical configurationas of the core. He suggests that experimental determination of these VCD spectra will confirm all of their absolute configurations.

Table 1. Experimental and computed optical rotation for 1-4 at the sodium D line.

^aRef. 8. ^bRef. 9. ^cRef. 10. ^eRef. 5. ^eRef. 11

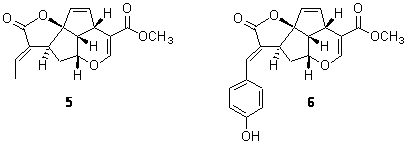
A second study involved the iridoids 5 and 6.⁷ Plumericin 5 has the absolute configuration shown below with [α]_D = +204. The more recently discovered prismatomerin 6 has [α]_D = -136, suggesting that the core polycyclic portion may have opposite absolute configuration. Stephens prepared the acetate of 6 and experimentally determined its VCD spectrum. The VCD spectrum was then computed using the above protocol. The computed spectrum for the enantiomer with the same absolute configuration as 5 matches the experimental spectrum. Thus, 5 and 6 have the same absolute configuration. Stephens concludes with the warning that optical activity of analogous compounds can be quite different and is not suitable for obtaining configuration information. Rather, VCD is a much more suitable test, especially when experimental and computed spectra are utilized.

I will finish this post with a brief recap of the optical rotation computations a few of the molecules discussed in a recent review by Crawford.¹² Crawford implements a linear-response coupled clusters with modified velocity gauge protocol. He compares the optical rotation computed with this method, the time-dependent DFT approach developed by Stephens et al and experiment. He describes systems where the CC approach performs much better than DFT, where DFT performs better than CC, but for the wrong reason, and a case where DFT appears to perform better than CC.

The optical rotation of (P)-(+)-[4]-triangulane 7 at a variety of wavelengths has been determined both experimentally and computationally. These results are listed in Table 2. It is readily apparent that CCSD performs much better than DFT. The poor performance of the DFT method is linked to electronic excitation energies that are too small.

Table 2. Optical rotation of 7.

^aRef. 13. ^bRef. 14.

The ORD of (S)-methyloxirane show a change of sign: -8.39 at 633 nm and +7.39 at 355 nm. CCSD predicts a reasonable value at 633 nm but gets the wrong sign at the shorter wavelength. On the other hand, B3LYP does predict the sign change. However, this seemingly correct result is due to (once again) underestimation of the excitation energy.

Lastly, Crawford reports on his study of (1S,4S)-norbornenone. The optical rotation of the sodium D line is -1146, and B3LYP does a very reasonable job in predicting a value of -1214. However, CCSD(MVG) grossly underestimates this value at -558. Though B3LYP again underestimates the excitation energy it appears to get the energy and rotational strength near the liquid-phase values. Most worrisome is that Crawford discounts basis set improvements and higher order correlation effects, and holds some hope for a significant difference in gas-phase vs solution phase rotations.

References

(1) Stephens, P. J., "Theory of Vibrational Circular Dichroism," J. Phys. Chem. 1985, 89, 748-752, DOI: 10.1021/j100251a006.

(2) Cheeseman, J. R.; Frisch, M. J.; Devlin, F. J.; Stephens, P. J., "Hartree-Fock
and Density Functional Theory ab Initio Calculation of Optical Rotation Using GIAOs: Basis Set
Dependence," J. Phys. Chem. A, 2000, 104, 1039-1046, DOI: 10.1021/jp993424s.

(3) Stephens, P. J.; Devlin, F. J.; Cheeseman,J. R.; Frisch, M. J., "Calculation of Optical Rotation Using Density Functional Theory," J. Phys. Chem. A, 2001, 105, 5356-5371, DOI: 10.1021/jp0105138.

(4) Stephens, P. J.; McCann, D. M.; Cheeseman, J. R.; Frisch, M. J., "Determination of absolute configurations of chiral molecules using ab initio time-dependent Density Functional Theory calculations of optical rotation: How reliable are absolute configurations obtained for molecules with small rotations?," Chirality, 2005, 17, S52-S64, DOI: 10.1002/chir.20109.

(5) Stephens, P. J.; McCann, D. M.; Devlin, F. J.; Smith, A. B., "Determination of the Absolute Configurations of Natural Products via Density Functional Theory Calculations of Optical Rotation, Electronic Circular Dichroism, and Vibrational Circular Dichroism: The Cytotoxic Sesquiterpene Natural Products Quadrone, Suberosenone, Suberosanone, and Suberosenol A Acetate," J. Nat. Prod., 2006, 69, 1055-1064, DOI: 10.1021/np060112p.

(6) Stephens, P. J.; Pan, J. J.; Devlin, F. J.; Urbanova, M.; Hajicek, J., "Determination of the Absolute Configurations of Natural Products via Density Functional Theory Calculations of Vibrational Circular Dichroism, Electronic Circular Dichroism and Optical Rotation: The Schizozygane Alkaloid Schizozygine," J. Org. Chem., 2007, 72, 2508-2524, DOI: http://dx.doi.org/10.1021/jo062567p.

(7) Stephens, P. J.; Pan, J. J.; Krohn, K., "Determination of the Absolute Configurations of Pharmacological Natural Products via Density Functional Theory Calculations of Vibrational
Circular Dichroism: The New Cytotoxic Iridoid Prismatomerin," J. Org. Chem., 2007, 72, 7641-7649, DOI: 10.1021/jo071183b.

(8) Smith, A. B.; Konopelski, J. P.; Wexler, B. A.; Sprengeler, P. A., "Quadrone structural and synthetic studies. Total synthesis of natural (-)-quadrone, the (+)-enantiomer, and the racemate. Conformational analysis, circular dichroism, and determination of absolute stereochemistry," J. Am. Chem. Soc., 1991, 113, 3533-3542, DOI: 10.1021/ja00009a047.

(9) Wijeratne, E. M. K.; Turbyville, T. J.; Zhang, Z.; Bigelow, D.; Pierson, L. S.; VanEtten, H. D.; Whitesell, L.; Canfield, L. M.; Gunatilaka, A. A. L., "Cytotoxic Constituents of Aspergillus terreus from the Rhizosphere of Opuntia versicolor of the Sonoran Desert," J. Nat. Prod., 2003, 66, 1567-1573, DOI: 10.1021/np030266u.

(10) Bokesch, H. R.; McKee, T. C.; Cardellina II, J. H.; Boyd, M. R., "Suberosenone, a new cytotoxin from Subergorgia suberosa," Tetrahedron Lett., 1996, 37, 3259-3262, DOI: 10.1016/0040-4039(96)00528-X

(11) Sheu, J. H.; Hung, K. C.; Wang, G. H.; Duh, C. Y., "New Cytotoxic Sesquiterpenes from the Gorgonian Isis hippuris," J. Nat. Prod., 2000, 63, 1603-1607, DOI: 10.1021/np000271n.

(12) Crawford, T. D.; Tam, M. C.; Abrams, M. L., "The Current State of Ab Initio Calculations of Optical Rotation and Electronic Circular Dichroism Spectra," J. Phys. Chem. A, 2007, 111, 12057-12068, DOI: 10.1021/jp075046u.

(13) Crawford, T. D.; Owens, L. S.; Tam, M. C.; Schreiner, P. R.; Koch, H., "Ab Initio Calculation of Optical Rotation in (P&)-(+)-[4]Triangulane," J. Am. Chem. Soc., 2005, 127, 1368-1369, DOI: 10.1021/ja042787p.

(14) de Meijere, A.; Khlebnikov, A. F.; Kozhushkov, S. I.; Kostikov, R. R.; Schreiner, P. R.; Wittkopp, A.; Rinderspacher, C.; Menzel, H.; Yufit, D. S.; Howard, J. A. K., "The First Enantiomerically Pure [n]Triangulanes and Analogues: σ-[n]Helicenes with Remarkable Features," Chem. Eur. J., 2002, 8, 828-842, DOI: 10.1002/1521-3765(20020215)8:4<828::AID-CHEM828>3.0.CO;2-Y

InChIs

1: InChI=1/C15H20O3/c1-14(2)7-15-9-4-3-8(14)10(15)5-12(16)11(15)6-18-13(9)17/h8-11H,3-7H2,1-2H3/t8?,9-,10?,11?,15?/m1/s1 PubChem
        InChIKey: BBIDMUQZCCGABN-UDZYVRSQBU

2: InChI=1/C15H22O/c1-9-5-6-11-12-7-13(16)10(2)15(9,12)8-14(11,3)4/h9,11-12H,2,5-8H2,1,3-4H3/t9-,11?,12?,15?/m0/s1
        InChIKey: JDGYVUJBJYXKSX-NCLPGTSEBA

3: InChI=1/C15H24O/c1-9-5-6-11-12-7-13(16)10(2)15(9,12)8-14(11,3)4/h9-12H,5-8H2,1-4H3/t9-,10+,11?,12?,15?/m0/s1
      InChIKey: KHINYKJYBNWSSP-BIGXPMCQBN

4: InChI=1/C17H26O2/c1-10-6-7-13-14-8-15(19-12(3)18)11(2)17(10,14)9-16(13,4)5/h10,13-15H,2,6-9H2,1,3-5H3/t10-,13?,14?,15+,17?/m0/s1
      InChIKey: UZRAQUNNGNYEHD-XDUGHSHMBF

5: InChI=1/C16H18O5/c1-3-8-11-6-12-13-9(10(7-20-12)14(17)19-2)4-5-16(11,13)21-15(8)18/h3,7,9,11-13H,4-6H2,1-2H3/b8-3+/t9-,11-,12-,13-,16-/m1/s1
      InChIKey: QOWSZGWHIKPQIA-WCDIAXTGBA
PubChem

6: InChI=1/C21H20O6/c1-25-19(23)15-10-26-17-9-16-14(8-11-2-4-12(22)5-3-11)20(24)27-21(16)7-6-13(15)18(17)21/h2-5,8,10,13,16-18,22H,6-7,9H2,1H3/b14-8+/t13-,16-,17-,18-,21-/m1/s1
      InChIKey: OXYVEVVOLQYXPZ-SOSYHPOKBY

7: InChI=1/C9H12/c1-2-7(1)5-9(7)6-8(9)3-4-8/h1-6H2
      InChIKey: JCHCWAJGYWGXMQ-UHFFFAOYAV

The Highlights article¹ in a recent issue of Angewandte Chemie Intermational Edition concerns the induced chirality of an achiral solvent by a chiral solute determining the overall optical activity. I blogged on this in my last post. This Highlights article stressed (as I did) the novelty of this effect and the need for further experiments and computation. I am sure that more will come in this exciting area.

It is also interesting to me that Angewandte would feature in this way one of its own articles. Isn’t the fact that it was accepted and then published in the journal sufficient stamp of its novelty and importance? Can anyone say “nepotism”?

References

(1) Neugebauer, J., “Induced Chirality in Achiral Media – How Theory Unravels Mysterious Solvent Effects,” Angew. Chem. Int. Ed., 2007, 46, 7738-7740, DOI: 10.1002/anie.200702858.

Bertran and Wipf have examined the role of solvent organization about a chiral molecule in producing the optical activity.¹ They generated 1000 configurations of benzene arrayed about methyloxirane from a Monte Carlo simulation. Each configuration was then constructed by keeping every benzene molecules within 0.5 nm from the center-of-mass of methyloxirane, usually 8-10 solvent molecules. The optical rotation was then computed at four wavelengths using TDDFT at BP86/SVP. (The authors note that though the Gaussian group recommends B3LYP/aug-ccpVDZ,^2-4 using the non-hybrid functional allows the use of resolution-of–the-identity⁵ techniques that make the computations about six orders of magnitude faster – of critical importance given the size of the clusters and the sheer number of them!) Optical rotation is then obtained by averaging over the ensemble.

The computed optical rotations disagree with the experiment by about 50% in magnitude but have the correct sign across the four different wavelengths. Use of the COSMO model (implicit solvent) provides the wrong sign at short wavelengths. But perhaps most interesting is that the computed optical activity of the solvent molecules in the configuration about the solute, but without including methyloxirane, is nearly identical to that of the whole cluster! In other words, the optical activity is due to the dissymmetric distribution of the solvent molecules about the chiral molecule, not the chiral molecule itself! It is the imprint of the chiral molecule on the solvent ordering that accounts for nearly all of the optical activity.

References

(1) Mukhopadhyay, P.; Zuber, G.; Wipf, P.; Beratan, D. N., "Contribution of a Solute’s
Chiral Solvent Imprint to Optical Rotation," Angew. Chem. Int. Ed. 2007,
46, 6450-6452, DOI: 10.1002/anie.200702273

(2) Stephens, P. J.; McCann, D. M.; Cheeseman, J. R.; Frisch, M. J., "Determination of
absolute configurations of chiral molecules using ab initio time-dependent Density Functional Theory calculations of optical rotation: How reliable are absolute configurations obtained for molecules with small rotations?," Chirality 2005, 17, S52-S64, DOI: 10.1002/chir.20109.

(3) Stephens, P. J.; Devlin, F. J.; Cheeseman, J. R.; Frisch, M. J., "Calculation of Optical Rotation Using Density Functional Theory," J. Phys. Chem. A 2001, 105, 5356-5371, DOI: 10.1021/jp0105138.

(4) Stephens, P. J.; McCann, D. M.; Devlin, F. J.; Flood, T. C.; Butkus, E.; Stoncius,
S.; Cheeseman, J. R., "Determination of Molecular Structure Using Vibrational Circular Dichroism Spectroscopy: The Keto-lactone Product of Baeyer-Villiger Oxidation of (+)-(1R,5S)-Bicyclo[3.3.1]nonane-2,7-dione," J. Org. Chem. 2005, 70, 3903-3913, DOI: 10.1021/jo047906y.

(5) Eichkorn, K.; Treutler, O.; Ohm, H.; Haser, M.; Ahlrichs, R., "Auxiliary Basis Sets to Approximate Coulomb Potentials," Chem. Phys. Lett. 1995, 240, 283-289, DOI: 10.1016/0009-2614(95)00621-A.

A growing area for the application of computational chemistry is in the structural identification of compounds. In the book, I discussed the use of computed IR spectra to identify intermediates in the photolysis of phenyl nitrene and carbine and the benzynes. In previous blogs, I have written posts (here, here and here) about recent use of computed NMR spectra to discern the structure of new natural products. With this post I discus the use of computed optical activity to determine the absolute configuration of molecules.

Rosini and co-workers have examined a number of oxygenated cyclohexene epoxides.to explore the use of TDDFT computed optical activity as a means for determining absolute configuration.¹ In chapter 1.6.3, I discuss the work of the Gaussian team on benchmarking optical rotation and ORD. They find that B3LYP/aug-cc-pVDZ computed optical activities are in quite reasonable agreement with experiment.^2-4 In this work, Rosini explores using a smaller basis set (6-31G(d)), the role of solvent, and also if computed spectra can be used to assess the absolute configuration of new molecules.

They first benchmark the B3LYP/6-31G(d) computed optical activities for a number of related cyclohexene epoxides against B3LYP/aug-cc-pVDZ and experimental values. I will begin by discussing two of their examples: (+)-chaloxone 1 (PubChem)
and (+)-epoxydon 2
(PubChem).

Five conformations of 1 were optimized in the gas phase and then their optical activities for the sodium D line were computed using TDDFT with both the small and larger basis set. These computations were then repeated to model the effect of solvent using PCM; the solution (methanol) B3LYP/6-31G(d) structures are shown in Figure 1.

1a 0.0	1b 2.40	1c 0.87
1d 1.02	1e 3.12

Figure 1. PCM(methanol)/B3LYP/6-31G(d) optimized structures of 1. Relative free energies of each conformer in kcal/mol.¹

The optical rotation at the sodium D line was then computed with TDDFT in both gas and solution phase with the smaller and larger basis set. The values were then averaged base on a Boltzmann weighting using the computed free energies of each conformer. The optical rotation for each conformer and the average values are listed in Table 1. The experimental optical rotation is +271. The authors note that while the gas phase B3LYP/6-31G(d) average value is far off the experimental value, it does predict the correct sign, and since all of the five conformers give rise to a positive rotation, any error in the energies will not affect the sign. The computed gas phase value with the larger basis set is in better agreement with experiment. However, it is still too large, but the solution values are much better. In fact, the PCM/B3LYP/aug-cc-pVDZ value is in excellent agreement with experiment.

Table 1. Computed optical activity of the conformers of 1 in gas and solution phase.

^aBased on a Boltzmann weighting of the population of each conformation.

Five conformers of epoxydon 2 were also located, and the computed solution structures are shown in Figure 2. The computed optical rotations for both the gas and solution phase for these structures (and the Boltzmann weighted averages) are listed in Table 2. The experimental value for the optical rotation of 2 is +93.

2a 0.0	2b 0.32	2c 0.23
2d 0.22	2e 0.66

Figure 2. PCM(methanol)/B3LYP/6-31G(d) optimized structures of 2. Relative free energies of each conformer in kcal/mol.¹

In this case, the small basis set performs very poorly. The gas phase B3LYP/6-31G(d) value
of [α]_D is -16, predicting the wrong sign, let alone the wrong magnitude. Things improve with the larger basis set, which predicts a value of +57. Since conformer 2ais levorotatory and the other four are dextrorotatory, the computed relative energies are key to getting the correct prediction. This is made even more poignant with the solution results, where the PCM/B3LYP/aug-cc-pVDZ prediction is quite acceptable.

Table 2. Computed optical activity of the conformers of 2 in gas and solution phase.

^aBased on a Boltzmann weighting of the population of each conformation.

Threy conclude with two examples of application of computation to assignment of structure. I discuss here the absolute configuration of (-)-sphaeropsidone 3 (PubChem).
Rosini located two conformations of 3, shown in Figure 3. The computed optical rotations are listed in Table 3. The experimental value for 3 is -130. Both conformers are computed to be dextrorotatory with all computational methods. The magnitude of the computed values using the larger basis set is in nice agreement with experiment, but the sign is wrong. Rosini concludes that the absolute configuration of 3 has been misassigned.

3a 0.06

3b 0.0

Figure 3. PCM(methanol)/B3LYP/6-31G(d) optimized structures of 3. Relative free energies of each conformer in kcal/mol.¹

Table 3. Computed optical activity of the conformers of 3 in gas and solution phase.

^aBased on a Boltzmann weighting of the population of each conformation.

References

(1) Mennucci, B.; Claps, M.; Evidente, A.; Rosini, C., "Absolute Configuration of Natural Cyclohexene Oxides by Time Dependent Density Functional Theory Calculation of the Optical Rotation: The Absolute Configuration of (-)-Sphaeropsidone and (-)-Episphaeropsidone Revised," J. Org. Chem. 2007, 72, 6680-6691, DOI: 10.1021/jo070806i

(2) Stephens, P. J.; Devlin, F. J.; Cheeseman, J. R.; Frisch, M. J., "Calculation of Optical Rotation Using Density Functional Theory," J. Phys. Chem. A 2001, 105, 5356-5371, DOI: 10.1021/jp0105138.

(3) Stephens, P. J.; McCann, D. M.; Cheeseman, J. R.; Frisch, M. J., "Determination of
absolute configurations of chiral molecules using ab initio time-dependent Density Functional Theory calculations of optical rotation: How reliable are absolute configurations obtained for molecules with small rotations?," Chirality 2005, 17, S52-S64, DOI: 10.1002/chir.20109.

(4) Stephens, P. J.; McCann, D. M.; Devlin, F. J.; Flood, T. C.; Butkus, E.; Stoncius,
S.; Cheeseman, J. R., "Determination of Molecular Structure Using Vibrational Circular Dichroism Spectroscopy: The Keto-lactone Product of Baeyer-Villiger Oxidation of (+)-(1R,5S)-Bicyclo[3.3.1]nonane-2,7-dione," J. Org. Chem. 2005, 70, 3903-3913, DOI: 10.1021/jo047906y.

InChI

1: InChI=1/C7H8O4/c1-10-4-2-3(8)6-7(11-6)5(4)9/h2-3,6-8H,1H3

2: InChI=1/C7H8O4/c8-2-3-1-4(9)6-7(11-6)5(3)10/h1,4,6-9H,2H2

3: InChI=1/C7H8O4/c1-10-4-2-3(8)6-7(11-6)5(4)9/h2,5-7,9H,1H3