Bickelhaupt and Houk present a nice review of their separately developed, but conceptually identical model for assessing reactivity.¹ Houk termed this the “distortion/interaction” model,² while Bickelhaupt named it “activation strain”.³ The concept is that the activation barrier can be dissected in a distortion or stain energy associated with bringing the reactants into the geometry of the transition state, and the interaction energy is the stabilization energy afforded by the molecular orbital interactions of the reactant components with each other in the transition state.

The review discusses a broad range of applications, including S_N2 and E₂ reactions, pericyclic reactions (including Diels-Alder reactions of enones and the dehdydro Diels-Alder reaction that I have discussed in this blog), a click reaction, a few examples involving catalysis, and the regioselectivity of indolyne (see this post). They also discuss the role of solvent and the relationship of this model to Marcus Theory.

I also want to mention in passing a somewhat related article by Jorgensen and co-authors published in the same issue of Angewandte Chemie as the above review.⁴ This article discusses the paucity of 10 electron cycloaddition reactions, especially in comparison to the large number of very important cycloaddition reactions involving 6 electrons, such as the Diels-Alder reaction, the Cope rearrangement, and the Claisen rearrangement. While the article does not focus on computational methods, computations have been widely used to discuss 10-electron cycloadditions. The real tie between this paper and the review discussed above is Ken Houk, whose graduate career started with an attempt to perform a [6+4] cycloaddition, and he has revisited the topic multiple times throughout his career.

References

1. Bickelhaupt, F. M.; Houk, K. N., "Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model." Angew. Chem. Int. Ed. 2017, 56, 10070-10086, DOI: 10.1002/anie.201701486.

2. Ess, D. H.; Houk, K. N., "Distortion/Interaction Energy Control of 1,3-Dipolar Cycloaddition Reactivity." J. Am. Chem. Soc. 2007, 129, 10646-10647, DOI: 10.1021/ja0734086

3. Bickelhaupt, F. M., "Understanding reactivity with Kohn-Sham molecular orbital theory: E2-S_N2 mechanistic spectrum and other concepts." J. Comput. Chem. 1999, 20, 114-128

4. Palazzo, T. A.; Mose, R.; Jørgensen, K. A., "Cycloaddition Reactions: Why Is It So
Challenging To Move from Six to Ten Electrons?" Angew. Chem. Int. Ed. 2017, 56, 10033-10038, DOI: 10.1002/anie.201701085.

Bispericyclic transition states arise when two pericyclic reactions merge to a common transition state. This leads to a potential energy surface with a bifurcation such that reactions that traverse this type of transition state will head towards two different products. The classic example is the dimerization of cyclopentadiene, involving two [4+2] Diels-Alder reactions. Unusual PESs are discussed in my book and in past blog posts.

Houk and coworkers have now identified a bispericyclic transition state involving two [6+4] cycloadditions.¹ Reaching back to work Houk pursued as a graduate student with Woodward for inspiration, these authors examined the reaction of tropone 1 with dimethylfulvene 2. Each moiety can act as the diene or triene component of a [6+4] allowed cycloaddition:

The product with fulvene 2 as the 6 π-e component and tropone as the 4 π-e component [6_F+4_T] is 3, while reversing their participation in the [6_T+4_F] cycloaddition leads to 4. A variety of [4+2] reactions are also possible. All of these reactions were investigated at PCM/M06-2X/6-311+G(d,p)//B3LYP-D3/6-31G(d). The reaction leading to 3 is exothermic by 3.0 kcal mol^-1, while the reaction to 4 endothermic by 1.3 kcal mol^-1.

Interestingly, there is only one transition state that leads to both 3 and 4, the first known bispericyclic transition state for two conjoined [6+4] cycloadditions. The barrier is 27.9 kcal mol^-1. The structures of the two products and the transition state leading to them are shown in Figure 1. 3 and 4 can interconvert through a Cope transition state, also shown in Figure 1, with a barrier of 26.3 kcal mol^-1 (for 4 → 3).

3	4
TS [6+4]	TS Cope

Figure 1. B3LYP-D3/6-31G(d) optimized geometries.

Given that a single transition leads to two products, the product distribution is dependent on the molecular dynamics. A molecular dynamics simulation at B3LYP-D3/6-31G(d) with 117 trajectories indicates that 4 is formed 91% while 3 is formed only 9%. Once again, we are faced with the reality of much more complex reaction mechanisms/processes than simple models would suggest.

References

1) Yu, P.; Chen, T. Q.; Yang, Z.; He, C. Q.; Patel, A.; Lam, Y.-h.; Liu, C.-Y.; Houk, K. N., "Mechanisms and Origins of Periselectivity of the Ambimodal [6 + 4] Cycloadditions of Tropone to Dimethylfulvene." J. Am. Chem. Soc. 2017, 139 (24), 8251-8258, DOI: 10.1021/jacs.7b02966.

InChIs

1: InChI=1S/C7H6O/c8-7-5-3-1-2-4-6-7/h1-6H
InChIKey=QVWDCTQRORVHHT-UHFFFAOYSA-N

2: InChI=1S/C8H10/c1-7(2)8-5-3-4-6-8/h3-6H,1-2H3
InChIKey=WXACXMWYHXOSIX-UHFFFAOYSA-N

3:InChI=1S/C15H16O/c1-15(2)10-6-8-12(14(16)9-7-10)11-4-3-5-13(11)15/h3-12H,1-2H3
InChIKey=SEKRUGIZAIQCDA-UHFFFAOYSA-N

4: InChI=1S/C15H16O/c1-9(2)14-10-7-8-11(14)13-6-4-3-5-12(10)15(13)16/h3-8,10-13H,1-2H3
InChIKey=AQQAMUGJSGJKLC-UHFFFAOYSA-N

A few nice review/opinion pieces have been piling up in my folder of papers of interest for this Blog. So, this post provides a short summary of a number of review articles that computationally-oriented chemists may find of interest.

Holy Grails in computational chemistry

Houk and Liu present a short list of “Holy Grails” in computationally chemistry.¹ They begin by pointing out a few technical innovations that must occur for the Grails to be found: development of a universal density functional; an accurate, generic force field; improved sampling for MD; and dealing with the combinatorial explosion with regards to conformations and configurations. Their list of Grails includes predicting crystal structures and structure of amorphous materials, catalyst design, reaction design, and device design. These Grails overlap with the challenges I laid out in my similarly-themed article in 2014.²

Post-transition state bifurcations and dynamics

Hare and Tantillo review the current understanding of post-transition state bifurcations (PTSB).³ This type of potential energy surface has been the subject of much of Chapter 8 of my book and many of my blog posts. What is becoming clear is the possibility of a transition state followed by a valley-ridge inflection leads to reaction dynamics where trajectories cross a single transition state but lead to two different products. This new review updates the state-of-the-art from Houk’s review⁴ of 2008 (see this post). Mentioned are a number of studies that I have included in this Blog, along with reactions involving metals, and biochemical systems (many of these examples come from the Tantillo lab). They close with the hope that their review might “inspire future studies aimed at controlling selectivity for reactions with PTSBs” (italics theirs). I might offer that controlling selectivity in these types of dynamical systems is another chemical Grail!

The Hase group has a long review of direct dynamics simulations.⁵ They describe a number of important dynamics studies that provide important new insight to reaction mechanism, such as bimolecular S_N2 reactions (including the roundabout mechanism) and unimolecular dissociation. They write a long section on post-transition state bifurcations, and other dynamic effects that cannot be interpreted using transition state theory or RRKM. This section is a nice complement to the Tantillo review.

Benchmarking quantum chemical methods

Mata and Suhm look at our process of benchmarking computational methods.⁶ They point out the growing use of high-level quantum computations as the reference for benchmarking new methods, often with no mention of any comparison to experiment. In defense of theoreticians, they do note the paucity of useful experimental data that may exist for making suitable comparisons. They detail a long list of better practices that both experimentalists and theoreticians can take to bolster both efforts, leading to stronger computational tools that are more robust at helping to understand and discriminate difficult experimental findings.

References

1) Houk, K. N.; Liu, F., "Holy Grails for Computational Organic Chemistry and Biochemistry." Acc. Chem. Res. 2017, 50 (3), 539-543, DOI: 10.1021/acs.accounts.6b00532.

2) Bachrach, S. M., "Challenges in computational organic chemistry." WIRES: Comput. Mol. Sci. 2014, 4, 482-487, DOI: 10.1002/wcms.1185.

3) Hare, S. R.; Tantillo, D. J., "Post-transition state bifurcations gain momentum – current state of the field." Pure Appl. Chem. 2017, 89, 679-698, DOI: 0.1515/pac-2017-0104.

4) Ess, D. H.; Wheeler, S. E.; Iafe, R. G.; Xu, L.; Çelebi-Ölçüm, N.; Houk, K. N., "Bifurcations on Potential Energy Surfaces of Organic Reactions." Angew. Chem. Int. Ed. 2008, 47, 7592-7601, DOI: 10.1002/anie.200800918

5) Pratihar, S.; Ma, X.; Homayoon, Z.; Barnes, G. L.; Hase, W. L., "Direct Chemical Dynamics Simulations." J. Am. Chem. Soc. 2017, 139, 3570-3590, DOI: 10.1021/jacs.6b12017.

6) Mata, R. A.; Suhm, M. A., "Benchmarking Quantum Chemical Methods: Are We Heading in the Right Direction?" Angew. Chem. Int. Ed. 2017, ASAP, DOI: 10.1002/anie.201611308.

Following on previous work (see these posts on ladderane and hexaphenylethane), Schreiner, Grimme and co-workers have examined the structure of the all-meta tri(di-t-butylphenyl)methane dimer 1₂.¹ In the study of hexaphenylethane,² Schreiner and Grimme note that t-butyl groups stabilize highly congested structures through dispersion, identifying them as “dispersion energy donors”.³ The idea here is that the dimer of 1 will be stabilized by these many t-butyl groups. In fact, the neutron diffraction study of the crystal structure of 1₂ shows an extremely close approach of the two methane hydrogens of only 1.566 Å, the record holder for the closest approach of two formally non-bonding hydrogen atoms.

To understand the nature of this dimeric structure, they employed a variety of computational techniques. (Shown in Figure 1 is the B3LYPD3^ATM(BJ)/def2-TZVPP optimized geometry of 1₂.) The HSE-3c (a DFT composite method) optimized crystal structure predicts the H^…H distance is 1.555 Å. The computed gas phase structure lengthens the distance to 1.634 Å, indicating a small, but essential, role for packing forces. Energy decomposition analysis of 1₂ at B3LYP-D3^ATM(BJ)/def2-TZVPP indicates a dominant role for dispersion in holding the dimer together. While 1₂ is bound by about 8 kcal mol^-1, the analogue of 1₂ lacking all of the t-butyl groups (the dimer of triphenylmethane 2₂) is unbound by over 8 kcal mol^-1. Topological electron density analysis does show a bond critical point between the two formally unbound hydrogen atoms, and the noncovalent interaction plot shows an attractive region between these two atoms.

Figure 1. ATM(BJ)/def2-TZVPP optimized geometry of 1₂, with most of the hydrogens suppressed for clarity. (Selecting the molecule will launch Jmol with the full structure, including the hydrogens.)

References

1) Rösel, S.; Quanz, H.; Logemann, C.; Becker, J.; Mossou, E.; Cañadillas-Delgado, L.; Caldeweyher, E.; Grimme, S.; Schreiner, P. R., "London Dispersion Enables the Shortest Intermolecular Hydrocarbon H···H Contact." J. Am. Chem. Soc. 2017, 139, 7428–7431, DOI: 10.1021/jacs.7b01879.

2) Grimme, S.; Schreiner, P. R., "Steric Crowding Can Stabilize a Labile Molecule: Solving the Hexaphenylethane Riddle." Angew. Chem. Int. Ed. 2011, 50 (52), 12639-12642, DOI: 10.1002/anie.201103615.

3) Grimme, S.; Huenerbein, R.; Ehrlich, S., "On the Importance of the Dispersion Energy for the Thermodynamic Stability of Molecules." ChemPhysChem 2011, 12 (7), 1258-1261, DOI: 10.1002/cphc.201100127.

InChIs

1: InChI=1S/C43H64/c1-38(2,3)31-19-28(20-32(25-31)39(4,5)6)37(29-21-33(40(7,8)9)26-34(22-29)41(10,11)12)30-23-35(42(13,14)15)27-36(24-30)43(16,17)18/h19-27,37H,1-18H3
InChIKey=VFNQDWKFTWSJAU-UHFFFAOYSA-N

The Schreiner group has again reported an amazing experimental and computational study demonstrating a fascinating quantum mechanical tunneling effect, this time for the trifluoromethylhydroxycarbene (CF₃COH) 2.¹ (I have made on a number of posts discussing a series of important studies in this field by Schreiner.) Carbene 2 is formed, in analogy to many other hydroxycarbenes, by flash vapor pyrolysis of the appropriate oxoacid 1 and capturing the products on a noble gas matrix.

Carbene 2t is observed by IR spectroscopy, and its structure is identified by comparison with the computed CCSD(T)/cc-pVTZ frequencies. When 2t is subjected to 465 nm light, the signals for 2t disappear within 30s, and two new species are observed. The first species is the cis conformer 2c, confirmed by comparison with its computed CCSD(T)/cc-pVTZ frequencies. This cis conformer remains even with continued photolysis. The other product is determined to be trifluoroacetaldehyde 3. Perhaps most interesting is that 2t will convert to 3 in the absence of light at temperatures between 3 and 30 K, with a half-life of about 144 h. There is little rate difference at these temperatures. These results are quite indicative of quantum mechanical tunneling.

To aid in confirming tunneling, they computed the potential energy surface at CCSD(T)/cc-pVTZ. The trans isomer is 0.8 kcal mol^-1 lower in energy that the cis isomer, and this is much smaller than for other hydroxycarbenes they have examined. The rotational barrier TS1 between the two isomer is quite large, 26.4 kcal mol^-1, precluding their interchange by classical means at matrix temperatures. The barrier for conversion of 2t to 3 (TS2) is also quite large, 30.7 kcal mol^-1, and insurmountable at 10K by classical means. No transition state connecting 2c to 3 could be located. These geometries and energies are shown in Figure 1.

2c 0.8

TS1 26.4

2t 0.0

TS2 30.7

3 -49.7

Figure 1. Optimized geometries at CCSD(T)/cc-pVTZ. Relative energies (kcal mol^-1) of each species are listed as well.

WKB computations at M06-2X/6-311++G(d,p) predict a half-life of 172 h, in nice agreement with experiment. The computed half-life for deuterated 2t is 10⁶ years, and the experiment on the deuterated analogue revealed no formation of deuterated 3.

The novel component of this study is that tunneling is conformationally selective. The CF₃ group stabilizes the cis form probably through some weak H^…F interaction, so that the cis isomer can be observed, but no tunneling is observed from this isomer. Only the trans isomer has the migrating hydrogen atom properly arranged for a short hop over to the carbon, allowing the tunneling process to take place.

References

1) Mardyukov, A.; Quanz, H.; Schreiner, P. R., "Conformer-specific hydrogen atom tunnelling in trifluoromethylhydroxycarbene." Nat. Chem. 2017, 9, 71–76, DOI: 10.1038/nchem.2609.

InChIs

1: =1S/C3HF3O3/c4-3(5,6)1(7)2(8)9/h(H,8,9)
InChIKey=GVDJEHMDNREMFA-UHFFFAOYSA-N

2: InChI=1S/C2HF3O/c3-2(4,5)1-6/h6H
InChIKey=FVJVNIREIXAWKU-UHFFFAOYSA-N

3: InChI=1S/C2HF3O/c3-2(4,5)1-6/h1H
InChIKey=JVTSHOJDBRTPHD-UHFFFAOYSA-N

Cyclopropyl rings can be joined together in a spiro fashion to form triangulanes. An interesting topology can be made by joining the rings to form a helical pattern, as shown in the [9]triangulane 1 below. Allen, Quanz, and Schreiner¹ have examined the notion of an infinite helical molecule formed in this way.

First, they describe how one can generate the coordinates of such a beast using a closed analytical expression, which is a really nice demonstration of applied geometry. Next, they compute the geometry of a series of [n]triangulanes at M06-2x/6-31G(d). The geometries of [9]triangulane and their largest example, [42]triangulane 2 are shown in Figure 1.

1

2

Figure 1. M06-2x/6-31G(d) optimized geometries of 1 and 2.

They show that the geometry of 2 exhibits a structure that has two different C-C distances: one between the spiro carbons, and the second between the spiro carbon and the methylene carbon. The distance between the spiro carbons is rather short (1.458 Å), suggesting that the bonding here is between carbons that are nearly sp²-hybridized.

Lastly, they discuss the thermodynamics of polytriangulane. They employ a series of homodesmotic reactions to attempt to determine the enthalpy for adding another cyclopropyl ring to an extended triangulane. Unfortunately, the computed enthalpy is quite dependent on functional used. Similar attempts to define the strain energy is also flawed in this way. However, regardless of the functional the enthalpy for adding a cyclopropane ring appears to reach an asymptote rather quickly. So, using [3]triangulane they estimate that the strain energy per mole of cyclopropane in triangulane is about 42.7 kcal mol^-1, or about 14 kcal mol^-1 of strain due to the spiroannulation.

References

(1) Allen, W. D.; Quanz, H.; Schreiner, P. R. “Polytriangulane,” J. Chem. Theory Comput. 2016, 12, 4707–4716, DOI: 10.1021/acs.jctc.6b00669.

InChIs

1: InChI=1S/C19H22/c1-2-12(1)5-14(12)7-16(14)9-18(16)11-19(18)10-17(19)8-15(17)6-13(15)3-4-13/h1-11H2/t14-,15-,16-,17-,18-,19-/m0/s1
InChIKey=XBTZCZDSKVTALB-DYKIIFRCSA-N

Enzyme SpnF is implicated in catalyzing the putative [4+2] cycloaddition taking 1 into 3. Houk, Singleton and co-workers have now examined the mechanism of this transformation in aqueous solution but without the enzyme.¹ As might be expected, this mechanism is not straightforward.

Reactant 1, transition states, and products 2 and 3 were optimized at SMD(H2O)/M06-2X/def2-TZVPP//B3LYP-D3(BJ)//6-31+G(d,p). Geometries and relative energies are shown in Figure 1. The reaction 1 → 2 is a formal [6+4] cycloaddition, and the reaction 1 → 3 is a formal [4+2] cycloaddition. Interestingly, only a single transition state could be located TS1. It is a bispericyclic TS (see Chapter 4 of my book), where these two pericyclic reaction sort of merge together. After TS1 is traversed the potential energy surface bifurcates, leading to 2 or 3. This is yet again an example of a single TS leading to two different products. (See the many posts I have written on this topic.) The barrier height is 27.6 kcal mol^-1, with 2 lying 13.1 kcal mol^-1 above 3. However, the steepest descent pathway from TS1 leads to 2. There is a second transition state TScope that describes a Cope rearrangement between 2 and 3. Using the more traditional TS theory description, 1 undergoes a [6+4] cycloaddition to form 2 which then crosses a lower barrier (TScope) to form the thermodynamically favored 3, which is the product observed in the enzymatically catalyzed reaction.

1 (0.0)
TS1 (27.6)
2 (4.0)	3 (-9.1)
(24.7)

Figure 1. B3LYP-D3(BJ)//6-31+G(d,p) optimized geometries and relative energies in kcal mol^-1.

Molecular dynamics computations were performed on this system by tracking trajectories starting in the neighborhood of TS1 on a B3LYP-D2/6-31G(d) PES. The results are that 63% of the trajectories end at 2, 25% end at 3, and 12% recross back to reactant 1, suggesting an initial formation ratio for 2:3 of 2.5:1. The reactions are very slow to cross through the “transition zone”, typically 2-3 times longer than for a usual Diels-Alder reaction (see this post).

Once again, we see an example of dynamic effects dictating a reaction mechanism. The authors pose a tantalizing question: Can an enzyme control the outcome of an ambimodal reaction by altering the energy surface such that the steepest downhill path from the transition state leads to the “desired” product(s)? The answer to this question awaits further study.

References

(1) Patel, A; Chen, Z. Yang, Z; Gutierrez, O.; Liu, H.-W.; Houk, K. N.; Singleton, D. A. “Dynamically
Complex [6+4] and [4+2] Cycloadditions in the Biosynthesis of Spinosyn A,” J. Amer. Chem. Soc. 2016, 138, 3631-3634, DOI: 10.1021/jacs.6b00017.

InChIs

1: InChI=1S/C24H34O5/c1-3-21-15-12-17-23(27)19(2)22(26)16-10-7-9-14-20(25)13-8-5-4-6-11-18-24(28)29-21/h4-11,16,18-21,23,25,27H,3,12-15,17H2,1-2H3/b6-4+,8-5+,9-7+,16-10+,18-11+/t19-,20+,21-,23-/m0/s1
InChIKey=JEKALMRMHDPSQK-ZTRRSECRSA-N

2: InChI=1S/C24H34O5/c1-3-19-8-6-10-22(26)15(2)23(27)20-12-11-17-14-18(25)13-16(17)7-4-5-9-21(20)24(28)29-19/h4-5,7,9,11-12,15-22,25-26H,3,6,8,10,13-14H2,1-2H3/b7-4-,9-5+,12-11+/t15-,16-,17-,18-,19+,20+,21-,22+/m1/s1
InChIKey=AVLPWIGYFVTVTB-PTACFXJJSA-N

3: InChI=1S/C24H34O5/c1-3-19-5-4-6-22(26)15(2)23(27)11-10-20-16(9-12-24(28)29-19)7-8-17-13-18(25)14-21(17)20/h7-12,15-22,25-26H,3-6,13-14H2,1-2H3/b11-10+,12-9+/t15-,16+,17-,18-,19+,20-,21-,22+/m1/s1
InChIKey=BINMOURRBYQUKD-MBPIVLONSA-N

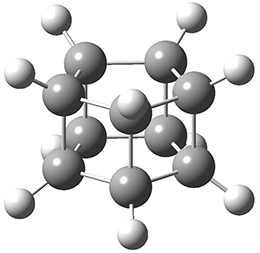
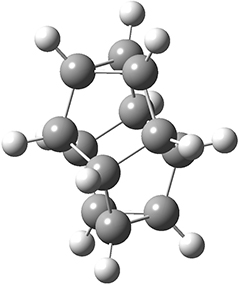
I have been delinquent in writing about the dehydro-Diels-Alder reactions, but really can’t put it off any further. These sets of reactions really deserve a fuller analysis than I am going to summarize here, but this post will provide a good jumping off point for anyone interested in further investigation.

So the Diels-Alder reaction is among the most famous and most important reactions in organic chemistry. The reaction creates a 6-member ring and sets up to four stereocenters. In the past couple of years many chemists have expressed interest in the variant where the four-carbon component is more highly unsaturated, i.e. enyne or diyne. I will summarize the results of three recent computational papers dealing with the reaction of a diyne with an yne.

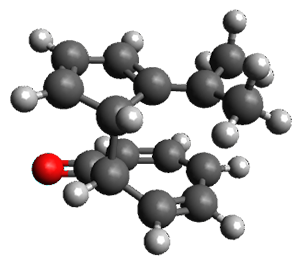
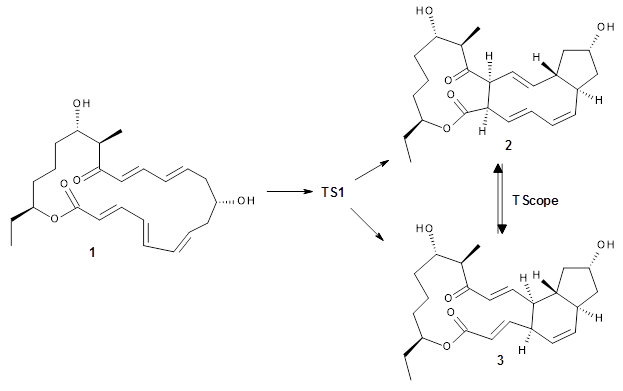
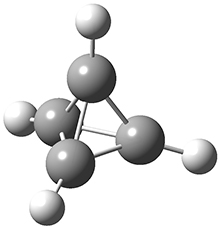
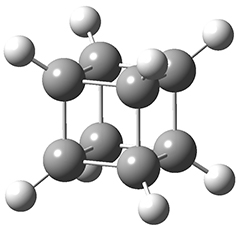
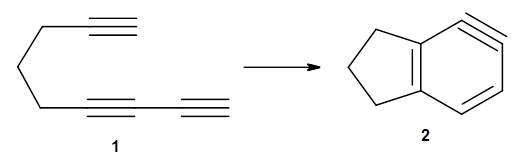
The first paper is by Skraba-Joiner, Johnson, and Agarwal.¹ They discuss, among a number of interesting pericyclic reactions, the intramolecular Diels-Alder reaction of triyne 1 to give 2. They examined a concerted and stepwise pathway at (U)M05-2X/6-311+G(d,p) and find the concerted to be favored by 6.0 kcal mol^-1. CCSD(T) using these geometries increases the difference to 8.2 kcal mol^-1. The T₁ diagnostic is fairly large for both the concerted and stepwise transition states, so they also performed CCSD(T)/CBS computations, which had much lower T₁ values. The concerted TS remained favorable, but by only 2.7 kcal mol^-1.

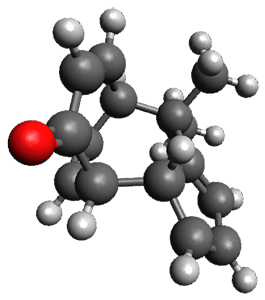
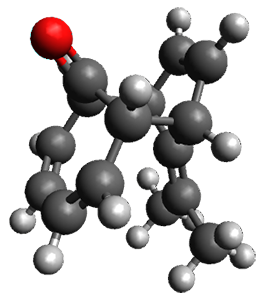
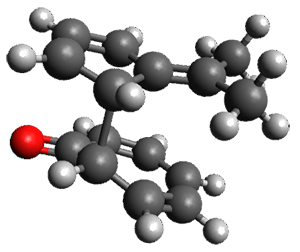
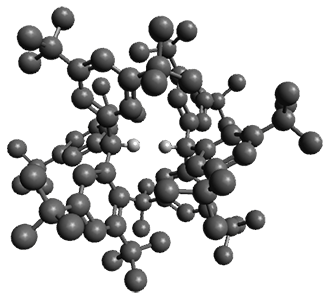
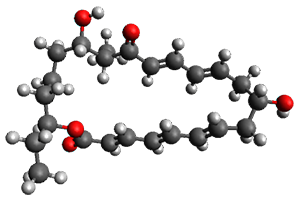
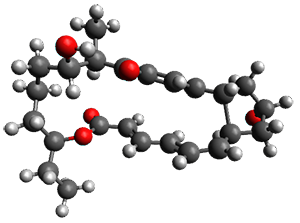
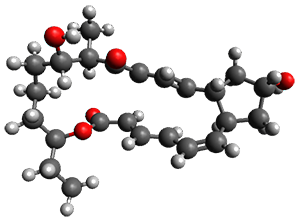
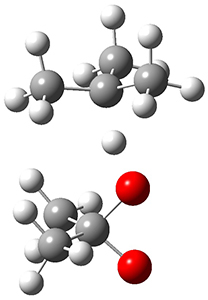
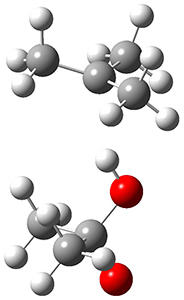
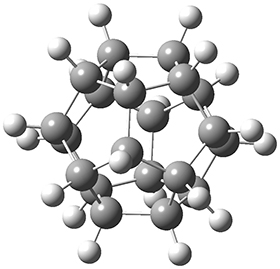
In the same special issue of the Journal of Organic Chemistry, Cramer, Hoye, and Kuwata examined a reaction closely related to what Johnson examined above.² They looked at the reaction taking 3 into 4 via both experiments and computations. The M06-2x/6-311+G(d,p) geometries for the concerted and first TS along the stepwise path (with R1=R2=H) are shown in Figure 1. Evaluating the energies at SMD(o-dichlorobenzene)/B3LYP-D3BJ/6-311+G-(d,p)//M06-2X/6-311+G(d,p) find in this case (along with all of the other R1/R2 variants they examined) that the stepwise path has a lower barrier than the concerted path. In the case where R1=R2=H, the stepwise path is favored by 6.0 kcal mol^-1. Additionally, these stepwise barriers are in reasonable agreement with the experimentally-derived barriers.

Concerted TS

Stepwise TS

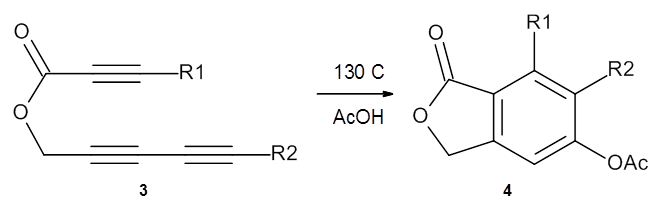
Figure 1. M06-2x/6-311+G(d,p) optimized geometries of the concerted and stepwise TSs for the reaction of 3H going to 4H.

It should be pointed out that the wavefunctions for the concerted TSs were all found to be unstable with regard to a restricted to unrestricted relaxation. Given this problem, they also performed a CASPT2 energy evaluation of the concerted and stepwise transition states for the case R1=R2=H. CASPT2 finds the stepwise barrier to be 3.7 kcal mol^-1 lower than the concerted barrier.

The last paper comes from the Houk lab, and examines the simplest set of intermolecular dehdro-Diels-Alder reactions.³ I will focus here on the most unsaturated analogue, the reaction of 1,3-butadiyne 5 with ethyne to give benzyne 6.

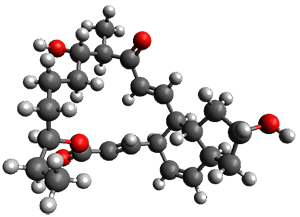
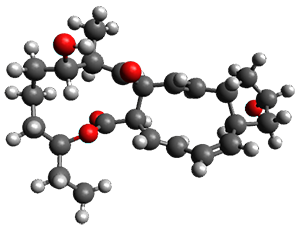
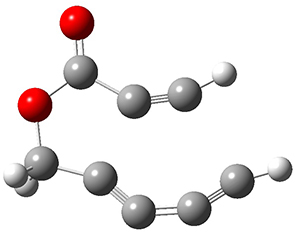
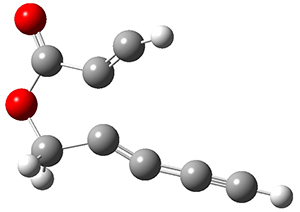
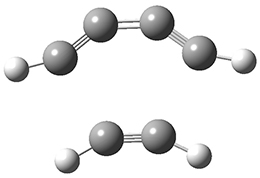
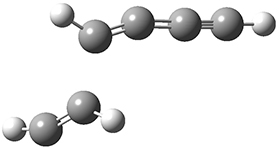
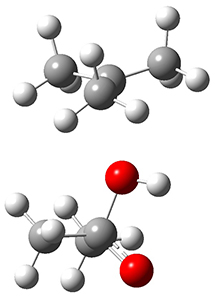
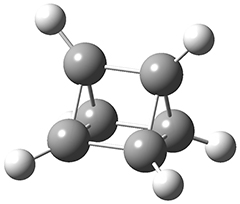
The concreted and stepwise transition states for this reaction (at (U)M06-2X/6-311+G(d,p)) are shown in Figure 2. The concerted barrier is 36.0 kcal moml^-1 while the stepwise barrier is slightly lower: 35.2 kcal mol^-1. The distortion energy for the concerted reaction is large (43.2 kcal mol^-1) due mostly to angle changes in the diyne. Its interaction energy is -7.2 kcal mol^-1, similar to the interaction energy in other similar Diels-Alder reactions. In contrast, the distortion energy for the stepwise pathway is 27.5 kcal mol^-1, but the interaction energy is +7.7 kcal mol^-1. These values are very similar to the distortion and interaction energy of the related (but less saturated DA reactions).

Concerted TS

Stepwise TS

Figure 2. (U)M06-2X/6-311+G(d,p) optimized concerted and stepwise TS for the reaction of 1,3-diyne with ethyne.

Molecular dynamics trajectories for both the concerted and stepwise paths reveal interesting differences. The concerted trajectories show an oscillatory behaviour of bending the angles at the C2 and C3 carbons prior to the TS, and then near synchronous formation of the new C-C bonds. The trajectories initiated at the stepwise TS show no systematic motion. Once the bond is formed, the biradical exhibits a long lifetime, on the order of picoseconds, much longer than the trajectory runs.

These three studies indicate the nature of the dehydro Diels-Alder reaction is very sensitive to reaction conditions, substituents, solvation, and all other manner of effects and will likely prove an area of interest for some time. It should keep a number of computational chemists busy for some time!

References

(1) Skraba-Joiner, S. L.; Johnson, R. P.; Agarwal, J. "Dehydropericyclic Reactions: Symmetry-Controlled Routes to Strained Reactive Intermediates," J. Org. Chem. 2015, 80, 11779-11787, DOI: 10.1021/acs.joc.5b01488.

(2) Marell, D. J.; Furan, L. R.; Woods, B. P.; Lei, X.; Bendelsmith, A. J.; Cramer, C. J.; Hoye, T. R.; Kuwata, K. T. "Mechanism of the Intramolecular Hexadehydro-Diels–Alder Reaction," J. Org. Chem. 2015, 80, 11744-11754, DOI: 10.1021/acs.joc.5b01356.

(3) Yu, P.; Yang, Z.; Liang, Y.; Hong, X.; Li, Y.; Houk, K. N. "Distortion-Controlled Reactivity and Molecular Dynamics of Dehydro-Diels–Alder Reactions," J. Am. Chem. Soc. 2016, 138, 8247-8252, DOI: 10.1021/jacs.6b04113.

InChIs

1: InChI=1S/C9H8/c1-3-5-7-9-8-6-4-2/h1-2H,5,7,9H2
InChIKey=IYZAZSVBWMMSLQ-UHFFFAOYSA-N

2: InChI=1S/C9H8/c1-2-5-9-7-3-6-8(9)4-1/h1,4H,3,6-7H2
InChIKey=PZJMTUKDGZUDBH-UHFFFAOYSA-N

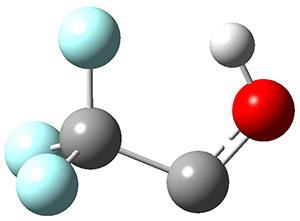
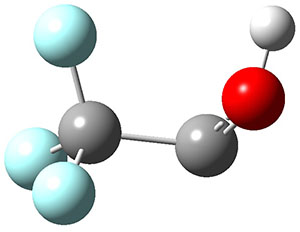
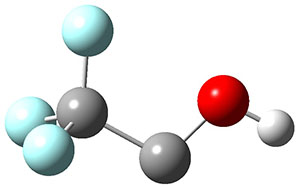
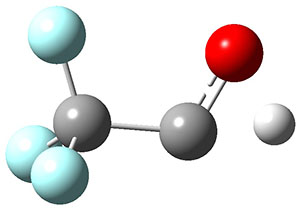
3H: InChI=1S/C8H4O2/c1-3-5-6-7-10-8(9)4-2/h1-2H,7H2
InChIKey=MGXDIFXPYGGQLF-UHFFFAOYSA-N

4H: InChI=1S/C10H8O4/c1-6(11)14-8-2-3-9-7(4-8)5-13-10(9)12/h2-4H,5H2,1H3
InChIKey=GEFLHLNIKGXWCA-UHFFFAOYSA-N

5: InChI=1S/C4H2/c1-3-4-2/h1-2H
InChIKey=LLCSWKVOHICRDD-UHFFFAOYSA-N

6: InChI=1S/C6H4/c1-2-4-6-5-3-1/h1-4H
InChIKey=KLYCPFXDDDMZNQ-UHFFFAOYSA-N

Dimethyldioxirane can oxidize alkanes to alcohols. The mechanism for the oxidation has been controversial, ranging from concerted, to radical intermediates to an H-abstraction—O-rebound mechanism. Yang, Yu, and Houk now offer a molecular dynamics examination of the reaction of dimethyldioxirane with isobutane.¹

Gas–phase (U)B3LYP/6-311++G(d,p)//(U)B3LYP/6-31G(d) computations give critical points outlined in the reaction below. The structures of the transition states and the intermediate are shown in Figure 1.

TS1 26.6 (25.9)	INT 8.6 (9.3)
TS2 8.6 (-0.8)

Figure 1. (U)B3LYP/6-31G(d) optimized geometries of TS1, INT, and TS2. Relative free energies (kcal mol^-1) in the gas (top) and solution (bottom) phases

The PES indicates a rebound mechanism, though in acetone solution phase, there was no transition state located for the second step; it appears to be barrierless. It should be noted that the size of the barrier is very small even in the gas phase. The energy given in Figure 1 is for the gas phase structure computed in solution.

Trajectories for both gas and solution phase were computed. For the gas phase, about 90% of the trajectories lead to separated radicals, but in an acetone about 90% of the trajectories lead directly to the alcohol, with only 10% leading to radicals. Even so, the acetone trajectories divide into two types, a dynamically concerted path where the time gap between the formation of the new C-O and O-H bonds is less than 60 fs, and a dynamically stepwise path where the time gap is greater than 60 fs, though for the trajectories that lead to product the gap is typically still less than 150 fs.

References

(1)  Yang, Z.; Yu, P.; Houk, K. N. "Molecular Dynamics of Dimethyldioxirane C–H Oxidation," J. Am. Chem. Soc. 2016, 138, 4237-4242, DOI: 10.1021/jacs.6b01028.

InChIs

Dimethyldioxirane: InChI=1S/C3H6O2/c1-3(2)4-5-3/h1-2H3
InChIKey=FFHWGQQFANVOHV-UHFFFAOYSA-N

Isobutane: InChI=1S/C4H10/c1-4(2)3/h4H,1-3H3
InChIKey=NNPPMTNAJDCUHE-UHFFFAOYSA-N

Karton, Schreiner, and Martin have benchmarked the heats of formation of some Platonic Solids and related hydrocarbons.¹ The molecules examined are tetrahedrane 1, cubane 2, dodecahedrane 3, trisprismane 4, pentaprismane 5, and octahedrane 6.

The optimized structures (B3LYP-D3BJ/def2-TZVPP) of these compounds are shown in Figure 1.

1	2
3	4
5	6

Figure 1. B3LYP-D3BJ/def2-TZVPP optimized geometries of 1-6.

Using the W1-F12 and W2-F12 composite methods, the estimated the heats of formation of these hydrocarbons are listed in Table 1. Experimental values are available only for 2 and 3; the computed values are off by about 2 kcal mol^-1, which the authors argue is just outside the error bars of the computations. They suggest that the experiments might need to be revisited.

Table 1. Heats of formation (kcal mol^-1) of 1-6.

They conclude with a comparison of strain energies computed using isogyric, isodesmic, and homodesmotic reactions with a variety of computational methods. Somewhat disappointingly, most DFT methods have appreciable errors compared with the W1-F12 results, and the errors vary depend on the chemical reaction employed. However, the double hybrid method DSD-PBEP86-D3BJ consistently reproduces the W1-F12 results.

References

(1)  Karton, A.; Schreiner, P. R.; Martin, J. M. L. "Heats of formation of platonic hydrocarbon cages by means of high-level thermochemical procedures," J. Comput. Chem. 2016, 37, 49-58, DOI: 10.1002/jcc.23963.

InChIs

1: InChI=1S/C4H4/c1-2-3(1)4(1)2/h1-4H
InChIKey=FJGIHZCEZAZPSP-UHFFFAOYSA-N

2: InChI=1S/C8H8/c1-2-5-3(1)7-4(1)6(2)8(5)7/h1-8H
InChIKey=TXWRERCHRDBNLG-UHFFFAOYSA-N

3: InChI=1S/C20H20/c1-2-5-7-3(1)9-10-4(1)8-6(2)12-11(5)17-13(7)15(9)19-16(10)14(8)18(12)20(17)19/h1-20H
InChIKey=OOHPORRAEMMMCX-UHFFFAOYSA-N

4: InChI=1S/C6H6/c1-2-3(1)6-4(1)5(2)6/h1-6H
InChIKey=RCJOMOPNGOSMJU-UHFFFAOYSA-N

5: InChI=1S/C10H10/c1-2-5-3(1)7-8-4(1)6(2)10(8)9(5)7/h1-10H
InChIKey=TXSUZIHPJIZTJT-UHFFFAOYSA-N

6: InChI=1S/C12H12/c1-2-4-6-5(11-7(1)10(4)11)3(1)9-8(2)12(6)9/h1-12H
InChIKey=DUDCBTWUEJEMGD-UHFFFAOYSA-N