Corannulene 1 is an interesting aromatic compound because it is nonplanar, having a bowl shape. [6]helicene is an interesting aromatic compound because it is nonplanar, having the shape of a helix. Kato, Segawa, Scott and Itami have joined these together to synthesize the interesting quintuple helicene compound 3.¹

The optimized structure of 3 is shown in Figure 1. They utilized computations to corroborate two experimental findings. First, the NMR spectra of 3 shows a small number of signals indicating that the bowl inversion should be rapid. The molecule has C₅ symmetry due to the bowl shape of the corannulene core. Rapid inversion makes the molecule effectively D₅. (The inversion transition state is of D₅ symmetry, and would be a nice quiz question for those looking for molecules of unusual point groups.) The B3LYP/6-31G(d) computed bowl inversion barrier is only 1.9 kcal mol^-1, significantly less that the bowl inversion barrier of 1: 10.4 kcal mol^-1. This reduction is partly due to the shallower bowl depth of 3 (0.572 Å in the x-ray structure, 0.325 Å in the computed structure) than in 1 (0.87 Å).

Figure 1. Optimized structure of 3.

Second, they took the enhanced MMMMM-isomer and heated it to obtain the thermodynamic properties for the inversion to the PPPPP-isomer. (The PPPPP-isomer is shown in the top scheme.) The experimental values are ΔH^‡ = 36.8 kcal mol^-1, ΔS^‡ = 8.7 cal mol^-1 K^-1, and ΔG^‡ = 34.2 kcal mol^-1 at 298 K. They computed all of the stereoisomers of 3 along with the transition states connecting them. The largest barrier is found in going from MMMMM–3 to MMMMP–3 with a computed barrier of 34.5 kcal mol^-1, in nice agreement with experiment.

References

1. Kato, K.; Segawa, Y.; Scott, L. T.; Itami, K., "A Quintuple [6]Helicene with a Corannulene Core as a C₅-Symmetric Propeller-Shaped π-System." Angew. Chem. Int. Ed. 2018, 57, 1337-1341, DOI: 10.1002/anie.201711985.

InChIs

1: InChI=1S/C20H10/c1-2-12-5-6-14-9-10-15-8-7-13-4-3-11(1)16-17(12)19(14)20(15)18(13)16/h1-10H
InChIKey=VXRUJZQPKRBJKH-UHFFFAOYSA-N

2: InChI=1S/C26H16/c1-3-7-22-17(5-1)9-11-19-13-15-21-16-14-20-12-10-18-6-2-4-8-23(18)25(20)26(21)24(19)22/h1-16H
InChIKey=UOYPNWSDSPYOSN-UHFFFAOYSA-N

3: InChI=1S/C80H40/c1-11-31-51-41(21-1)42-22-2-12-32-52(42)62-61(51)71-63-53-33-13-3-23-43(53)44-24-4-14-34-54(44)64(63)73-67-57-37-17-7-27-47(57)48-28-8-18-38-58(48)68(67)75-70-60-40-20-10-30-50(60)49-29-9-19-39-59(49)69(70)74-66-56-36-16-6-26-46(56)45-25-5-15-35-55(45)65(66)72(62)77-76(71)78(73)80(75)79(74)77/h1-40H
InChIKey=XYUIBQJVZTYREY-UHFFFAOYSA-N

The structure of (+)-frondosin B 1 has been the subject of some concern. The compound has been synthesized by a number of research groups with the expected R isomer as the target. However, the Danishefsky¹ and MacMillan² synthesis led to a molecule with [α]_D of about +16°, while Trauner³ reports a value of -16.8° and Ovaska⁴ prepared the S isomer with [α]_D = -17.3°. Something is amiss here.

Joyce and coworkers have looked into this structure problem through a combination of advanced analytical techniques and computational chemistry.⁵ They utilize optical activity, electronic circular dichroism (ECD) and vibrational circular dichroism (VCD) and compare the experiments with computational results. IR and VCD were computed at B3LYP/6-31G** using a Boltzmann-weighted set of low-energy conformations. ECD computations were done at CAM-B3LYP/6-31++G**//B3LYP/6-31G**.

Basically, they found that (+)-frondosin B does have the R stereocenter. The different synthetic schemes did actually all lead to the same isomer, tested by looking at key intermediates along the way. The discrepancy in the optical activity is due to a small impurity, 2, that has the opposite rotation and a magnitude 10 times greater than that of authentic 1.

This paper is another nice example demonstrating the power of modern computational approaches to spectra that can be extremely valuable in structure determination. Organic chemists of all stripes should certainly be aware of how this tool can complement experiments.

My thanks to Derek Lowe who posted on this paper in his In The Pipeline blog.

References

1) Inoue, M.; Carson, M. W.; Frontier, A. J.; Danishefsky, S. J., "Total Synthesis and Determination of the Absolute Configuration of Frondosin B." J. Am. Chem. Soc.
2001, 123, 1878-1889, DOI: 10.1021/ja0021060.

2) Reiter, M.; Torssell, S.; Lee, S.; MacMillan, D. W. C., "The organocatalytic three-step total synthesis of (+)-frondosin B." Chem. Sci. 2010, 1, 37-42, DOI: 10.1039/C0SC00204F.

3) Hughes, C. C.; Trauner, D., "Palladium-catalyzed couplings to nucleophilic heteroarenes: the total synthesis of (−)-frondosin B." Tetrahedron 2004, 60, 9675-9686, DOI: 10.1016/j.tet.2004.07.041.

4) Ovaska, T. V.; Sullivan, J. A.; Ovaska, S. I.; Winegrad, J. B.; Fair, J. D., "Asymmetric Synthesis of Seven-Membered Carbocyclic Rings via a Sequential Oxyanionic 5-Exo-Dig Cyclization/Claisen Rearrangement Process. Total Synthesis of (−)-Frondosin B." Org. Letters 2009, 11, 2715-2718, DOI: 10.1021/ol900967j.

5) Joyce, L. A.; Nawrat, C. C.; Sherer, E. C.; Biba, M.; Brunskill, A.; Martin, G. E.; Cohen, R. D.; Davies, I. W., "Beyond optical rotation: what’s left is not always right in total synthesis." Chem. Sci. 2018, 9, 415-424, DOI: 10.1039/C7SC04249C.

InChIs

1: InChI=1S/C20H24O2/c1-12-6-8-16-14(5-4-10-20(16,2)3)18-15-11-13(21)7-9-17(15)22-19(12)18/h7,9,11-12,21H,4-6,8,10H2,1-3H3/t12-/m1/s1
InChIKey=LSPMJSWSYGOLFD-GFCCVEGCSA-N

2: InChI=1S/C20H24O2/c1-12-5-4-10-20(3)16(12)8-6-13(2)19-18(20)15-11-14(21)7-9-17(15)22-19/h7,9,11,13,21H,4-6,8,10H2,1-3H3/t13-,20-/m1/s1
InChIKey=ZBXZDKMLFIJFHG-ZUOKHONESA-N

The Grimme group has examined all 1812 C₆₀ isomers, in part to benchmark some computational methods.¹ They computed all of these structures at PW6B95-D3/def2-QZVP//PBE-D3/def2-TZVP. The lowest energy structure is the expected fullerene 1 and the highest energy structure is the nanorod 2 (see Figure 1).

Figure 1. Optimized structures of the lowest (1) and highest (2) energy C₆₀ isomers.

About 70% of the isomers like in the range of 150-250 kcal mol^-1 above the fullerene 1, and the highest energy isomer 2 lies 549.1 kcal mol^-1 above 1. To benchmark some computational methods, they selected the five lowest energy isomers and five other isomers with higher energy to serve as a new database (C60ISO), with energies computed at DLPNO-CCSD(T)/CBS*. The mean absolute deviation of the PBE-D3/def2-TZVP relative energies with the DLPNO-CCSD(T)/CBS* energies is relative large 10.7 kcal mol^-1. However, the PW6B95-D3/def2-QZVP//PBE-D3/def2-TZVP method is considerably better, with a MAD of only 1.7 kcal mol^-1. This is clearly a reasonable compromise method for fullerene-like systems, balancing accuracy with computational time.

They also compared the relative energies of all 1812 isomers computed at PW6B95-D3/def2-QZVP//PBE-D3/def2-TZVP with a number of semi-empirical methods. The best results are with the DFTB-D3 method, with an MAD of 5.3 kcal mol^-1.

References

1) Sure, R.; Hansen, A.; Schwerdtfeger, P.; Grimme, S., "Comprehensive theoretical study of all 1812 C₆₀ isomers." Phys. Chem. Chem. Phys. 2017, 19, 14296-14305, DOI: 10.1039/C7CP00735C.

InChIs

1: InChI=1S/C60/c1-2-5-6-3(1)8-12-10-4(1)9-11-7(2)17-21-13(5)23-24-14(6)22-18(8)28-20(12)30-26-16(10)15(9)25-29-19(11)27(17)37-41-31(21)33(23)43-44-34(24)32(22)42-38(28)48-40(30)46-36(26)35(25)45-39(29)47(37)55-49(41)51(43)57-52(44)50(42)56(48)59-54(46)53(45)58(55)60(57)59
InChIKey=XMWRBQBLMFGWIX-UHFFFAOYSA-N

2: InChI=1S/C60/c1-11-12-2-21(1)31-41-32-22(1)3-13(11)15-5-24(3)34-43(32)53-55-47-36-26-6-16-17-7(26)28-9-19(17)20-10-29-8(18(16)20)27(6)37-46(36)54(51(41)55)52-42(31)33-23(2)4(14(12)15)25(5)35-44(33)58-56(52)48(37)39(29)50-40(30(9)10)49(38(28)47)57(53)59(45(34)35)60(50)58
InChIKey=AGZHNPDQKMDYHI-UHFFFAOYSA-N

Click chemistry has been used in a broad range of applications. The use of metal catalysts has limited its application to biological system, but the development of strain-promoted cycloaddition to cyclooctyne has opened up click chemistry to bioorthogonal labeling.

An interesting variation on this is the use of 1,2-benzoquinone 1 and substituted analogues as the Diels-Alder diene component. Escorihuela and co-workers have reported on the use of this diene with a number of cyclooctyne derivatives, measuring kinetics and also using computations to assess the mechanism.¹

Their computations focused on two reactions using cyclooctyne 2 and the cyclopropane-fused analogue 3:

They examined these reactions with a variety of density functionals along with some post-HF methods. The transition states of the two reactions are shown in Figure 1. A variety of different density functionals and MP2 are consistent in finding synchronous or nearly synchronous transition states.

Figure 1. B97D/6-311+G(d,p) transition states for Reactions 1 and 2.

In terms of activation energies, all of the DFT methods consistently overestimate the barrier by about 5-10 kcal mol^-1, with B97D-D3 doing the best. MP2 drastically underestimates the barriers, though the SOS-MP2 or SCS-MP2 improve the estimate. Both CCSD(T) and MR-AQCC provide estimates of about 8.5 kcal mol^-1, still 3-4 kcal mol^-1 too high. The agreement between CCSD(T), a single reference method, and MR-AQCC, a multireference method, indicate that the transition states have little multireference character. Given the reasonable estimate of the barrier afforded by B97D-D3, and its tremendous performance advantage over SCS-MP2, CCSD(T) and MR-AQCC, this is the preferred method (at least with current technology) for examining Diels-Alder reactions like these, especially with larger molecules.

References

1) Escorihuela, J.; Das, A.; Looijen, W. J. E.; van Delft, F. L.; Aquino, A. J. A.; Lischka, H.; Zuilhof, H., "Kinetics of the Strain-Promoted Oxidation-Controlled Cycloalkyne-1,2-quinone Cycloaddition: Experimental and Theoretical Studies." J. Org. Chem. 2018, 83, 244-252, DOI: 10.1021/acs.joc.7b02614.

InChIs

1: InChI=1S/C6H4O2/c7-5-3-1-2-4-6(5)8/h1-4H
InChIKey=WOAHJDHKFWSLKE-UHFFFAOYSA-N

2: InChI=1S/C8H12/c1-2-4-6-8-7-5-3-1/h1-6H2
InChIKey=ZPWOOKQUDFIEIX-UHFFFAOYSA-N

3: InChI=1S/C9H12/c1-2-4-6-9-7-8(9)5-3-1/h8-9H,3-7H2
InChIKey=rQDNSAFCVPAMWCJ-UHFFFAOYSA-N

4: InChI=1S/C14H16O2/c15-13-11-7-8-12(14(13)16)10-6-4-2-1-3-5-9(10)11/h7-8,11-12H,1-6H2
InChIKey=OQMYZEFKUMPECV-UHFFFAOYSA-N

5: InChI=1S/C15H16O2/c16-14-12-5-6-13(15(14)17)11-4-2-9-7-8(9)1-3-10(11)12/h5-6,8-9,12-13H,1-4,7H2/t8-,9+,12?,13?
InChIKey=NKDGTIVNLDJQKR-RFZWMSCOSA-N

Computed NMR spectra have become a very useful tool in identifying chemical structures. I have blogged on this multiple times. A recent trend has been the development of computational procedures that lead to computed spectra (again, see that above link). Now, Grimme, Neese and coworkers have offered their approach to computed NMR spectra, including spin-spin splitting.¹

Their procedure involves four distinct steps.

1. Generation of the conformer and rotamer space. This is a critical distinctive element of their method in that they take a number of different tacks for sampling conformational space to insure that they have identified all low-energy structures. This involves a combination of normal mode following, genetic structure crossing (based on genetic algorithms for optimization), and molecular dynamics. Making this all work is their choice of using the computational efficient GFN-xTB² quantum mechanical method.
2. The low-energy structures are then subjected to re-optimization at PBEh-3c and then single-point energies obtained at DSD-BLYP-D3/def2-TZVPP including treatment of solvation by COSMO-RS. The low-energy structures that contribute 4% or more of the Boltzmann-weighted population are then carried forward.
3. Chemical shifts and spin-spin coupling constants are then computed with the PBE0 method and the pcS and pcJ basis sets developed by Jensen for computing NMR shifts.³
4. Lastly, the chemical shifts and coupling constants are averaged and the spin Hamiltonian is solved.

The paper provides a number of examples of the application of the methodology, all with quite good success. The computer codes to run this method are available for academic use from xtb@thch.uni-bonn.de.

References

1) Grimme, S.; Bannwarth, C.; Dohm, S.; Hansen, A.; Pisarek, J.; Pracht, P.; Seibert, J.; Neese, F., "Fully Automated Quantum-Chemistry-Based Computation of Spin–Spin-Coupled Nuclear Magnetic Resonance Spectra." Angew. Chem. Int. Ed. 2017, 56, 14763-14769, DOI: 10.1002/anie.201708266.

2) Grimme, S.; Bannwarth, C.; Shushkov, P., "A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86)." J. Chem. Theory Comput. 2017, 13, 1989-2009, DOI: 10.1021/acs.jctc.7b00118.

3) Jensen, F., "Basis Set Convergence of Nuclear Magnetic Shielding Constants Calculated by Density Functional Methods." J. Chem. Theory Comput. 2008, 4, 719-727, DOI: 10.1021/ct800013z.

I seem to be recently flooded with papers dealing with tunneling in organic systems. Well, here’s one more! Kozuch, Borden, Schreiner and co-workers seek out systems whereby isotopic substitution might lead to reaction selectivity.¹ Their base system is cyclopropylmethylcarbene 1, which can undergo three different reactions: (a) the ring can expand to give 1-methylcyclobut-1-ene 2, (b) a hydrogen can shift from the terminal methyl group to give vinylcyclopropane 3, or (c) the methane hydrogen can shift to produce ethylidenecyclopropane 4. This last option can be neglected since its barrier (20.5 kcal mol^-1) is so much higher than for the other two, 7.5 kcal mol^-1 for the ring expansion and 12.1 kcal mol^-1 for the [1,2]H-shift converting 1 → 3.

At high temperature, the ring expansion to 2 will dominate, but at low temperature the hydrogen shift to 3 might dominate by tunneling through the barrier due to the low mass and short distances involved. The reaction rates were computed using B3LYP/6-31G(d,p) and small-curvature tunneling. At low temperature, the rate for the hydrogen shift is 10 orders of magnitude faster than the ring expansion. Thinking that deuterium substitution of the terminal methyl group might slow down the rate of the [1,2]-shift, they computed the rates for the reactions of 1-d3, and in fact the rate of this shift does reduce by 10⁴ but it is still much faster than the rate for ring expansion. What is needed is a system where the rate for ring expansion is slower than the rate for hydrogen migration but faster than the rate of deuterium migration.

They examine a number of different substituents that may help to lower the barrier for the ring expansion. The methoxy derivative 5 turns out to suit the bill perfectly. The methoxy group reduces the barrier for ring expansion from 7.5 kcal mol^-1 with 1 to 2.5 kcal mol^-1 with 5. With hydrogenated 5, the [1,2]H-shift is 10³ times faster than ring expansion, but with deuterated 5, ring expansion is twice as fast as the deuterium migration.

The authors call this isotope controlled selectivity (ICS), and this is the first example of this type of control.

References

1. Nandi, A.; Gerbig, D.; Schreiner, P. R.; Borden, W. T.; Kozuch, S., Isotope-Controlled Selectivity by Quantum Tunneling: Hydrogen Migration versus Ring Expansion in Cyclopropylmethylcarbenes. J. Am. Chem. Soc. 2017, 139, 9097-9099, DOI: 10.1021/jacs.7b04593.

InChIs

1: InChI=1S/C5H8/c1-2-5-3-4-5/h5H,3-4H2,1H3
InChIKey=KJIJNBZLGHBOTI-UHFFFAOYSA-N

2: InChIInChIKey=AVPHQXWAMGTQPF-UHFFFAOYSA-N

3: InChI=1S/C5H8/c1-2-5-3-4-5/h2,5H,1,3-4H2
InChIKey=YIWFBNMYFYINAD-UHFFFAOYSA-N

4: InChI=1S/C5H8/c1-2-5-3-4-5/h2H,3-4H2,1H3
InChIKey=ZIFNDRXSSPCNID-UHFFFAOYSA-N

5: InChI=1S/C6H10O/c1-3-6(7-2)4-5-6/h4-5H2,1-2H3
InChIKey=YMBSTCICUAORNN-UHFFFAOYSA-N

6: InChIInChIKey=QBLNAZHAVPMLHB-UHFFFAOYSA-N

7: InChIInChIKey=FHYLDABSPVPDTJ-UHFFFAOYSA-N

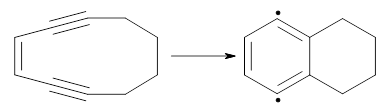
Antiaromatic compounds by definition are unstable and so difficult to prepare. One approach to increase their stability is to fuse aromatic ring(s) onto the antiaromatic system. I discuss in this blog post two different scaffolds where this approach has been successful in preparing molecules that express some degree of antiaromaticity. In addition, I mention a technique to aid in evaluating the aromatic/antiaromatic character.

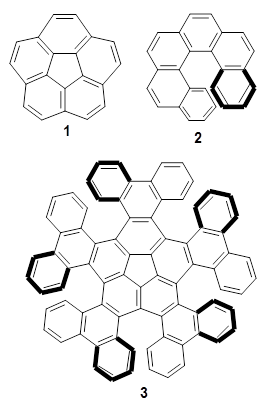
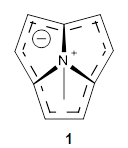
Pentalene 1 is a formal 8-π electron system and would be antiaromatic. To avoid this antiaromatic character, the double bonds are localized. Fusing benzenoid rings to pentalene to give dibenzo[a,e]penatalene 2 has been done, but the central rings avoid antiaromatic character by expressing the Kekule structure shown below.

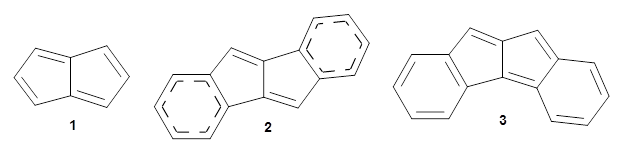
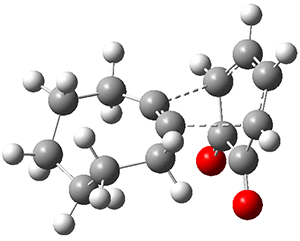
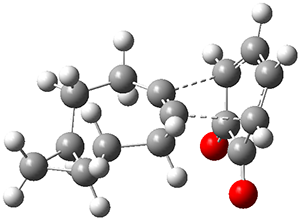
Yasuda and coworkers report the preparation of mesityl-substituted dibenzo[a,f]penatalene
3.¹ Resonance structures of 3¸ shown below, either have only one aromatic ring, or have two aromatic rings along with a trimethylenemethane (TMM) diradical component. Thus, one might expect 3 to express more antiaromatic character than 2.

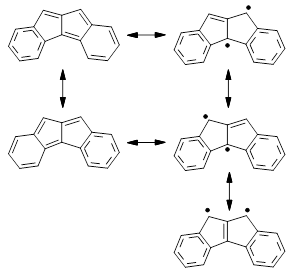
NICS(1) values, computed at B3LYP/6-31G**, for 2 are -6.23 for the 6-member ring and +5.87 ppm for the 5-member ring, showing reduced aromaticity of the former ring. In sharp contrast, the NICS(1) values for 3 are +7.48 for the 6-member ring and +25.5 ppm for the 5-member ring, indicating substantial antiaromatic character for both rings. The calculated spin density distribution shows largest unpaired density on the expected carbon atoms based on the resonance structures involving the TMM fragment.

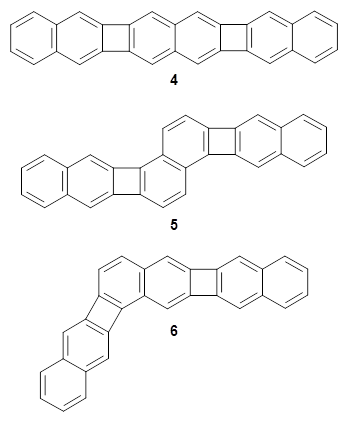
Xia and coworkers have prepared substituted analogues of the three structural isomers whereby three naphthylene units are fused together creating two cyclobutadienoid rings.² These three frameworks are molecules 4-6. The 4-member rings are formally antiaromatic, tempered by the fused aromatic naphthylene groups. The question is then how does the different attachment geometry manifest in aromatic and/or antiaromatic character?

The computations take advantage of the NICS-XY method – well, a variation of this method. I had meant to write a post about the NICS-XY method when Stanger published it,³ but I just never got around to it. The idea is that NICS is evaluated typically at a single point, and just which point to use has been the subject of some discussion. Instead, Stanger proposes the NICS-XY method as a grid of points perpendicular to the plane of the molecule, typically in the plane bisecting the molecule. Trends in the values as one moves across the ring and perpendicular to the ring could assist in identifying aromatic/antiaromatic behavior.

Xia computed the NICS_πZZ along a line in the molecular plane bisecting the rings. This is shown in the figure below, which I have reproduced from the article. For example, for 4, which is compound 1 in the Xia paper and the figure below, the NICS values are taken along the line that horizontally bisects the molecule. In ring A, the values are negative, indicative of an aromatic ring. Across ring B, the values are still negative, but not as negative as for ring A, indicating a diminished aromaticity. In ring C, the values are positive, as one would expect for the antiaromatic cyclobutadienoid ring.

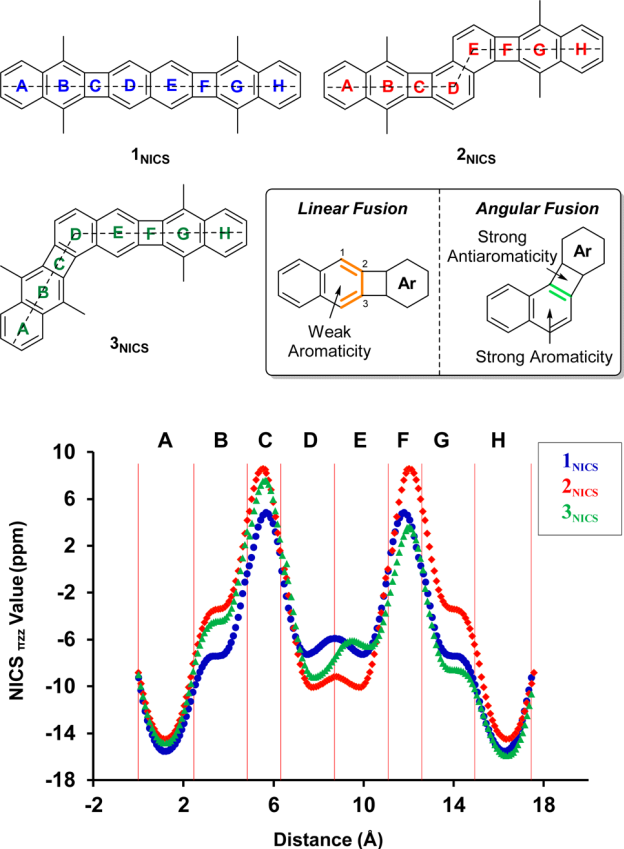
Figure taken from J. Am. Chem. Soc. 2017, 139, 15933-15939.

The authors highlight two trends. First, in the linear fusion (see the inset above), the aromatic ring fused to the cyclobutadienoid ring expresses diminished aromaticity. This can be understood in the following way. In naphthalene, the C2-C3 bond is longer than the C1-C2 bond. When the cyclobutadienoid is fused at the C2-C3 bond, it can lengthen even more to weaken the antiaaromaticity of the 4-member ring, and this consequently reduces the aromaticity of the 6-member ring. Fusion of the cyclobutadienoid ring at C1-C2, the shorter bond, causes a higher degree of antiaromaticity in the 4-member ring. The lengthening of this C1-C2 bond to try to reduce the antiromaticity of the 4-member ring leads to greater bond equalization in the 6-member ring, and its consequently greater aromatic character.

References

1. Konishi, A.; Okada, Y.; Nakano, M.; Sugisaki, K.; Sato, K.; Takui, T.; Yasuda, M., "Synthesis and Characterization of Dibenzo[a,f]pentalene: Harmonization of the Antiaromatic and Singlet Biradical Character." J. Am. Chem. Soc. 2017, 139, 15284-15287, DOI: 10.1021/jacs.7b05709.

2. Jin, Z.; Teo, Y. C.; Teat, S. J.; Xia, Y., "Regioselective Synthesis of [3]Naphthylenes and Tuning of Their Antiaromaticity." J. Am. Chem. Soc. 2017, 139, 15933-15939, DOI: 10.1021/jacs.7b09222.

3. Gershoni-Poranne, R.; Stanger, A., "The NICS-XY-Scan: Identification of Local and Global Ring Currents in Multi-Ring Systems." Chem. Eur. J. 2014, 20, 5673-5688, DOI: 10.1002/chem.201304307.

InChIs

1: InChI=1S/C8H6/c1-3-7-5-2-6-8(7)4-1/h1-6H
InChIKey=GUVXZFRDPCKWEM-UHFFFAOYSA-N

2: InChI=1S/C16H10/c1-3-7-13-11(5-1)9-15-14-8-4-2-6-12(14)10-16(13)15/h1-10H
InChIKey=OZEPXROCWSMGGM-UHFFFAOYSA-N

3: InChI=1S/C16H10/c1-3-7-14-11(5-1)9-13-10-12-6-2-4-8-15(12)16(13)14/h1-10H
InChIKey=XOERMEAUYMRNNZ-UHFFFAOYSA-N

4: InChI=1S/C30H16/c1-2-6-18-10-24-23(9-17(18)5-1)27-13-21-15-29-25-11-19-7-3-4-8-20(19)12-26(25)30(29)16-22(21)14-28(24)27/h1-16H
InChIKey=CHDMCKMZQIHGAH-UHFFFAOYSA-N

5: InChI=1S/C30H16/c1-3-7-19-15-27-25(13-17(19)5-1)23-11-9-22-21(29(23)27)10-12-24-26-14-18-6-2-4-8-20(18)16-28(26)30(22)24/h1-16H
InChIKey=LPXGODOTGXTPRU-UHFFFAOYSA-N

6: InChI=1S/C30H16/c1-2-7-19-13-26-25(12-18(19)6-1)27-15-21-9-10-22-24-11-17-5-3-4-8-20(17)14-29(24)30(22)23(21)16-28(26)27/h1-16H
InChIKey=BKMGPFRQJXDFJQ-UHFFFAOYSA-N

The range of aromatic compounds seems limitless. Mascal and co-workers have prepared the azatriquinacene 1 in a remarkably simple fashion.¹ The molecule is a zwitterion, with the carbon atoms forming a 9-center, but 10 π-electron ring, and the quaternary nitrogen sitting above it. The carbon ring satisfies Hückel’s rule (4n+2) and so should be aromatic. The capping nitrogen should help to keep the carbon ring fixed in a shallow bowl.

As expected, the molecule in fact turns out to possess an aromatic 10 π-electron ring. The B3LYP/6-311++G(d,p) geometry is shown in Figure 1. There is little bond alternation among the C-C distances: the mean deviation is only 0.015 Å with the largest difference only 0.024 &Aring. The x-ray crystal structure shows the same trends. The NICS(1) value is -12.31 ppm, larger even than that of benzene (-10.22 ppm).

Figure 1. B3LYP/6-311++G(d,p) geometry of 1.

References

1) Hafezi, N.; Shewa, W. T.; Fettinger, J. C.; Mascal, M., "A Zwitterionic, 10 π Aromatic Hemisphere." Angew. Chem. Int. Ed. 2017, 56, 14141-14144, DOI: 10.1002/anie.201708521.

InChIs

1: InChI=1S/C10H9N/c1-11-8-2-3-9(11)6-7-10(11)5-4-8/h2-7H,1H3
InChIKey=ZXZPLDVSQUVKTH-UHFFFAOYSA-N

Though recognized to occur in organic systems, the breadth of involvement of heavy-atom tunneling has not been established. Doubleday, Greer and coworkers have examined 13 simple organic reactions sampling pericyclic reactions, radical rearrangements and S_N2 reactions for heavy-atom tunneling.¹ A few of these reactions are shown below.

Reaction rates were obtained using the small curvature tunneling approximation (SCT), computed using Gaussrate. Reaction surfaces were computed at B3LYP/6-31G*. The tunneling correction to the rate was also estimated using the model developed by Bell: k_Bell = (u/2)/sin(u/2) where u = hν^‡/RT and ν^‡ is the imaginary frequency associated with the transition state. The temperature was chosen so as to give a common rate constant of 3 x 10^-5 s^-1. Interestingly, all of the examined reactions exhibited significant tunneling even at temperatures from 270-350 K (See Table 1). The tunneling effect estimated by Bell’s equation is very similar to that of the more computationally demanding SCT computation.

Table 1. Tunneling contribution to the rate constant

This study points towards a much broader range of reactions that may be subject to quantum mechanical tunneling than previously considered.

(Note: The original post had swapped some of the values in Table 1. These have now been corrected. My thanks to Drs. Greer and Doubleday for bringing this to my attention.)

References

1. Doubleday, C.; Armas, R.; Walker, D.; Cosgriff, C. V.; Greer, E. M., "Heavy-Atom Tunneling Calculations in Thirteen Organic Reactions: Tunneling Contributions are Substantial, and Bell’s Formula Closely Approximates Multidimensional Tunneling at ≥250 K." Angew. Chem. Int. Ed. 2017, 56, 13099-13102, DOI: 10.1002/anie.201708489.

Over the past nine years the Schreiner group, often in collaboration with the Allen group, have produced some remarkable studies demonstrating the role of tunneling control. (I have made quite a number of posts on this topics.) Tunneling control is a third mechanism for dictating product formation, in tandem with kinetic control (the favored product is the one that results from the lowest barrier) and thermodynamic control (the favored product is the one that has the lowest energy). Tunneling control has the favored product resulting from the narrowest mass-considered barrier.

Schreiner has written a very clear perspective on tunneling control. It is framed quite interestingly by some fascinating quotes:

It is probably fair to say that many organic chemists view the concept of tunneling, even of hydrogen atoms, with some skepticism. – Carpenter 1983²

Reaction processes have been considered as taking place according to the laws of classical mechanics, quantum mechanical theory being only employed in calculating interatomic forces. – Bell 1933³

Schreiner’s article makes it very clear how critical it is to really think about reactions from a truly quantum mechanical perspective. He notes the predominance of potential energy diagrams that focus exclusively on the relative energies and omits any serious consideration of the reaction coordinate metrics, like barrier width. When one also considers the rise in our understanding of the role of reaction dynamics in organic chemistry (see, for example, these many posts), just how long will it take for these critical notions to penetrate into standard organic chemical thinking? As Schreiner puts it:

It should begin by including quantum phenomena in introductory textbooks, where they are, at least in organic chemistry, blatantly absent. To put this oversight in words similar to those used much earlier by Frank Weinhold in a different context: “When will chemistry textbooks begin to serve as aids, rather than barriers, to this enriched quantum-mechanical perspective?”⁴

References

1) Schreiner, P. R., "Tunneling Control of Chemical Reactions: The Third Reactivity Paradigm." J. Am. Chem. Soc. 2017, 139, 15276-15283, DOI: 10.1021/jacs.7b06035.

2) Carpenter, B. K., "Heavy-atom tunneling as the dominant pathway in a solution-phase reaction? Bond shift in antiaromatic annulenes." J. Am. Chem. Soc. 1983, 105, 1700-1701, DOI: 10.1021/ja00344a073.

3) Bell, R. P., "The Application of Quantum Mechanics to Chemical Kinetics." Proc. R. Soc. London, Ser. A 1933, 139 (838), 466-474, DOI: 10.1098/rspa.1933.0031.

4) Weinhold, F., "Chemistry: A new twist on molecular shape." Nature 2001, 411, 539-541, DOI: 10.1038/35079225.