Suppose you are looking at the reaction aA + bB → cC + dD. You can compute each of these molecules at two computational levels; lets call these M1 and M2. Then the reaction energy is
Now, if the two computational methods are reasonably complete, then ΔEM1 ≈ ΔEM2. This can also be true if the reaction has been selected such that one might expect very good cancellation of errors. In this case, the overall problems in computing the reactants are similar to the problems computing the products, and so these problems (i.e., errors) will cancel off. So, if we have the latter condition (a reaction constructed to obtain excellent cancellation of errors), then we might be able to exploit this idea in order to obtain energies of large molecules with a large method while avoiding to actually have to do these very large computations!
How does this work? Let’s suppose the largest molecule in the reaction is molecule C. Since
then
and so
So, we can get the energy of the big molecule C at the big method M1 by computing the energy of the big molecule C at the smaller method M2 along with computing all of the other molecules at both levels. If these other molecules are significantly smaller than molecule C, there can be considerable time savings here. This is the idea presented in a recent article by Raghavachari.1
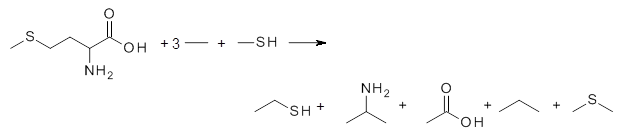
The key element here is a systematic means for generating appropriate reactions, ones that (a) involve small molecules other than the molecule of interest and (b) get good cancellation of errors. Raghavachari comes up with a systematic way of creating a reaction with ever larger reference molecules. This is analogous with the methodology presented by Wheeler, Schleyer and Allen.2 Basically, the method decomposes the molecule of interest into smaller molecules that preserve the immediate chemical environment around each heavy atom, a method they call CBH-2 (connectivity-based hierarchy). The reaction below is an example of the CBH-2 decomposition reaction for methionine. (Note that CBH-2 is essentially a homodesmotic reaction and CBH-3 is essentially the group equivalent reaction I defined years ago.3)
|
|
They apply the concept towards computing the energy of larger molecules (having 6-13 heavy atoms) at CCSD(T)/6-31+G(d,p) by only having to compute these large molecules at MP2/6-31+G(d,p). For a set of 30 molecules, the error in the energy of the extrapolated energy vs. the actual CCSD(T) energy is 0.35 kcal mol-1.
One of the advantages of this approach is that the small molecules are used over and over again, but they need be computed only twice, once at CCSD(T) and once at MP2.
This is certainly an approach that has been implicitly employed by many people for a long time, but here is made explicit and points towards ways to apply it even more widely.
References
(1) Ramabhadran, R. O.; Raghavachari, K. "Extrapolation to the Gold-Standard in Quantum Chemistry: Computationally Efficient and Accurate CCSD(T) Energies for Large Molecules Using an Automated Thermochemical Hierarchy," J. Chem. Theor. Comput. 2013, ASAP DOI: 10.1021/ct400465q.
(2) Wheeler, S. E.; Houk, K. N.; Schleyer, P. v. R.; Allen, W. D. “A Hierarchy of Homodesmotic Reactions for Thermochemistry,” J. Am. Chem. Soc. 2009, 131, 2547-2560, DOI: 10.1021/ja805843n.
(3) Bachrach, S. M. “The Group Equivalent Reaction: An Improved Method for Determining Ring Strain Energy,” J. Chem. Ed. 1990, 67, 907-908, DOI: 10.1021/ed067p90.

darren responded on 03 Dec 2013 at 4:54 am #
… and as the ‘small’ molecules begin to appear on figshare, they don’t even need to be calculated.
Ilie Fishtik responded on 04 Dec 2013 at 7:52 pm #
There are two major problems with this (and many similar) papers. The first one is the stoichiometric arbitrariness of reaction schemes. It looks like Raghavachari missed the recent discussion about arbitrariness vs. uniqueness of chemical reactions in computational thermochemistry (I. Fishtik, J. Phys. Chem. A, 2012, 116, 8792–8793; M. D. Wodrich et al, J. Phys. Chem. A, 2012, 116, 8794–8796). Otherwise, Raghavachari would easily observed that their reactions are also often arbitrary. The example of methionine cited by Steven in his post illustrates the issue in a straightforward manner. Thus, the following reaction among reference species may be envisioned
CH3CH3 + CH3CH3SH → CH3SH + CH3CH2CH3
Notice, this reaction conserves all possible groups present in reference species at the CBH-2 level. This reaction may be linearly combined in an infinite number of ways with the reaction proposed by Raghavachari resulting in an infinity of reactions. Unless the energy change of the above reaction is identically equal to zero, the energy/enthalpy of methionine may, thus, be adjusted to whatever value we want. Raghavachari’s mistake is that he employs more reference species that are needed to generate a uniquely balanced reaction. For instance, removing propane from the list of reference species it is still possible to write a balanced reaction among remaining species
CH3-S-CH2-CH2-CH(NH2)-COOH + 2 CH3-CH3 + 2CH3-SH
→ 2CH3-CH2-SH + CH3-CH(NH2)-CH3 + CH3-COOH + CH3-S-CH3
The second problem is more serious. Even though quantum chemical methods can produce decent results based on a single reaction scheme, these methods are still far from being exact. As a result, employing a minimal number of species is not justified. Just the opposite, using a single reaction is the worst case scenario. First, using a single reaction scheme implies that computational methods perform exactly for reference species. Therefore, increasing the number of reference species is the only way we can obtain a statistically comprehensive performance evaluation (error) of computational methods. Second, a larger number of reference species may reveal outliers among reference species and, as a consequence, a better prediction for target species.
The exact and unique solution of the problem for an arbitrary number of reference species is available (I. Fishtik, J. Phys. Chem. A, 2012, 116, 1854–1863). This solution is not some sort of interpretational concept that you may accept or you may not accept. Rather, it is a result that is as exact and unique as mass balance. As such, there is simply no way one can avoid it.
Thus, in the case of methionine we have two options. First, if we want to stay with a single and unique reaction scheme, then, we should remove one reference species from the list CH3-CH3, CH3-SH, CH3-CH2-CH3. Second, if we want to stay with all seven reference species, then, the exact solution is given as an weighted average over three group additivity response reactions. These are
1. CH3-S-CH2-CH2-CH(NH2)-COOH + 2 CH3-CH3 + 2CH3-SH
→ 2CH3-CH2-SH + CH3-CH(NH2)-CH3 + CH3-COOH + CH3-S-CH3
2. CH3-S-CH2-CH2-CH(NH2)-COOH + 4CH3-CH3
→ CH3-CH(NH2)-CH3 + CH3-COOH + 2CH3-CH2-CH3 + CH3-S-CH3
3. CH3-S-CH2-CH2-CH(NH2)-COOH + 4CH3-SH + 2CH3-CH2-CH3
→ CH3-CH2-SH + CH3-CH(NH2)-CH3 + CH3-COOH + CH3-S-CH3
Each of these reactions is characterized by a stoichiometric factor equal to 1, 2 and 1 for reaction 1, 2 and 3, respectively. As a result, reactions need to be generated in a game changing way. In particular, the freshman chemistry procedures of balancing chemical reactions are not valid anymore. If E1, E2 and E3 are the energies of methionine at M1 level obtained via reactions 1, 2 and 3 respectively, then, the exact value of the methionine energy at M1 is
E = 1/4(E1 + 2E2 + E3)