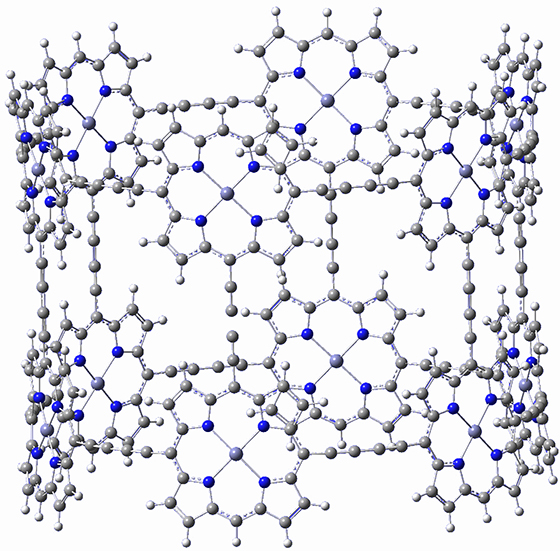
I don’t really have anything to say about this recent paper by Anderson, et al.1 They have simply prepared a very beautiful structure, an aryllated analogue of 1. They even optimized the structure of 1 at BLYP/6-31G(d) and it’s shown in Figure 1. That must have taken some time!
Figure 1. BLYP/6-31G(d) optimized structure of 1.
(Remember that you can manipulate this structure by simply clicking on in, which will launch the JMol app.)
References
(1) Neuhaus, P.; Cnossen, A.; Gong, J. Q.; Herz, L. M.; Anderson, H. L. "A Molecular Nanotube with Three-Dimensional π-Conjugation," Angew. Chem. Int. Ed. 2015, 54, 7344-7348, DOI: 10.1002/anie.201502735.

Henry Rzepa responded on 06 Aug 2015 at 12:33 am #
Beautiful indeed. Re: that must have taken some time! caught my eye. The following questions came to mind:
1. Yes, we do not know how much time, or what sort of resource was needed to do a 6-31G(d) calculation on a system with 480 atoms, including 12 zincs. It is useful to know this sort of stuff in case you want to replicate it or carry out similar calculations.
2. The 480 atom coordinates were split over pages 13-20 of the SI, with page breaks included. I had a go at extracting them from the PDF file (on a Mac). It tends to be a struggle (especially with double column formats which this one was not), but for reasons I did not solve, a copy operation followed by a paste into a text editor got me only 443 lines (I repeated this several times to check it was reproducible, some sort of buffer limit?). Basically, extracting text from PDF files can be quite a hit and miss process, depending on the software used, the OS, the size, etc etc.
3. The article reports some vibrational frequencies, including Herzberg-Teller modes, but there are 3N-6 = 1434 of them and we do not have access to any normal modes in the article other than in diagrammatic form. That is a lot of missing information (you might see where I am going with this one, ie FAIR data).
4. I am intrigued by the functional used, BLYP (dating from the very early days of DFT in the late 1980s). Why? And no dispersion correction.
5. I also noted that the SI reports that C1 symmetry (ie no symmetry) was used. Actually, this is not a trivial thing. I did manage to get the coordinates out of the Jmol instance above and found they symmetrize very easily to D2h symmetry. This reduces the basis functions from 6048 down to eight groups of symmetry adapted functions, each with 734-778 functions. Put simply, the calculation goes about eight times faster.
6.Depending on the resources available, a calculation with <800 symmetry adapted functions in each irreducible representation is not that difficult on a typical "commodity" box with say 20 processors and ~96 Gbytes of shared memory. The thing that really kills any such calculation is the frequencies, which indeed may take a few days (perhaps a week) to obtain.
I hope these comments cast a little light on the "state-of-the-art" calculations on large molecules. I would also argue that including a D3-Grimme like dispersion correction adds very little to the computational time and produces perhaps a more realistic answer.
Fabio Pichierri responded on 25 Jan 2016 at 10:15 pm #
Hi Henry, as for (4), with a pure (non-hybrid) functional one can improve the overall computational efficiency through the density-fitting approximation. Hence, with the same basis set (e.g., 6-31G(d) or else) the BLYP calculation is faster than the corresponding B3LYP one. As for not including the dispersion correction, well, the system contains many pi-electrons but I cannot see pi-pi interactions of some relevance. It would be interesting to compare the BLYP structure with one obtained from a modern semiempirical method, say PM6 or PM7.