Can one identify a labile bond in a molecule without computing activation barriers? Markopoulos and Grunenberg suggest that examination of the bond length and its associated relaxed force constant might provide some guidance.1
The relaxed force constant comes from identifying the force constant for some coordinate while allowing for other coordinates to relax. Badger’s rule relates the (normal) force constant to bond distance (k = a/(req – d)3). For a series of 36 molecules, covering 71 C-C single bonds, Badger’s rule fits the data well, except for a set of molecules which undergo rapid Cope rearrangements (like bullvalene and semibullvalene). For these molecules, the relaxed force constants are much lower than Badger’s rule predicts, and indicates a weakened bond. This gives rise to their low activation barriers.
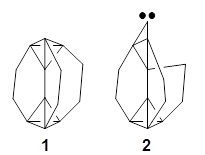
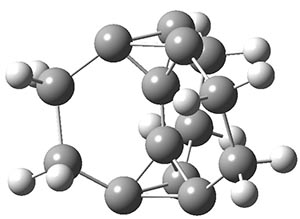
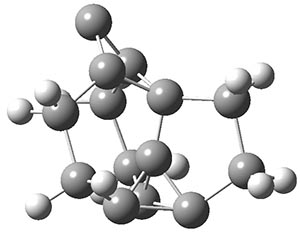
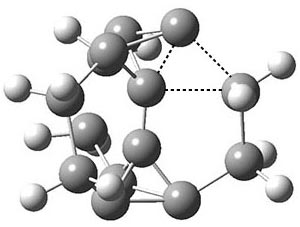
Another example is provided with the highly strained polycyclic hydrocarbon 1. This compound is predicted (B3LYP/6-31G(d)) to undergo a [1,2]-shift to give the carbene 2 (see Figure 1), and this is extremely exothermic: -105.7 kcal mol-1, reflecting the enormous strain of 1. The barrier, through TS1 (Figure 1), is only 6.7 kcal mol-1. This rearrangement was predicted by examining the relaxed force constants which identified a very weak bond, despite a short bond distance of 1.404 Å. It is unlikely that without this guidance, one would have predicted that this short bond is likely to rupture and produce this particular product.
|
1 |
2 |
|
TS1 |
|
Figure 1. B3LYP/6-31G(d) optimized structures of 1, 2, and TS1.
References
(1) Markopoulos, G.; Grunenberg, J. "Predicting Kinetically Unstable C-C Bonds from the Ground-State Properties of a Molecule," Angew. Chem. Int. Ed. 2013, 52, 10648-10651, DOI: 10.1002/anie.20130382.
InChIs
1: InChI=1S/C14H12/c1-2-8-11-5-3-9-7(1)10(9)4-6-12(8,11)14(8,11)13(7,9)10/h1-6H2
InChIKey=LNBZAENQMFDBJW-UHFFFAOYSA-N
2: InChI=1S/C14H12/c1-3-11-12-4-2-9-7-8(1,9)10(9)5-6-13(11,12)14(10,11)12/h1-6H2
InChIKey=UKVODHRLGFPZPT-UHFFFAOYSA-N

Henry Rzepa responded on 06 Dec 2013 at 10:49 am #
A famous example of the violation of Badger’s rule is of course Benzene. One of its normal vibrations, the so-called Kekule mode, which interconverts the two Kekule cyclohexatriene forms, is depressed (weaker) than Badger says it should be. I wonder if the relaxed force constants for this mode have been calculated?
Henry Rzepa responded on 06 Dec 2013 at 10:56 am #
I wonder if Bob Pascal’s S-H-H-Si system might contain the same effect? There, the H…H length is ~1.5Å but one might presume that this corresponds to a bond that is actually repulsive (although the NCI index computed in that region actually suggests otherwise). Here we would have a situation where the relaxed force constant for that diatomic pair might actually be negative, an extreme violation of Badger’s rule if you like.
To put it another way, bonds often have external constraints imposed upon them that have little to do with the electrons, and in these situations the force constant may not behave normally.
Henry Rzepa responded on 06 Dec 2013 at 11:01 am #
And finally, I would add that the little molecule C2, depending of course on how you regard the bonding, would be another controversial example of Badger’s rule violated.