I have written quite a number of posts on using quantum mechanics computations to predict NMR spectra that can aid in identifying chemical structure. Perhaps the most robust technique is Goodman’s DP4 method (post), which has seen some recent revisions (updated DP4, DP4+). I have also posted on the use of computed coupling constants (posts).
Grimblat, Gavín, Daranas and Sarotti have now combined these two approaches, using computed 1H and 13C chemical shifts and 3JHH coupling constants with the DP4 framework to predict chemical structure.1
They describe two different approaches to incorporate coupling constants:
- dJ-DP4 (direct method) incorporates the coupling constants into a new probability function, using the coupling constants in an analogous way as chemical shifts. This requires explicit computation of all chemical shifts and 3JHH coupling constants for all low-energy conformations.
- iJ-DP4 (indirect method) uses the experimental coupling constants to set conformational constraints thereby reducing the number of total conformations that need be sampled. Thus, large values of the coupling constant (3JHH > 8 Hz) selects conformations with coplanar hydrogens, while small values (3JHH < 4 Hz) selects conformations with perpendicular hydrogens. Other values are ignored. Typically, only one or two coupling constants are used to select the viable conformations.
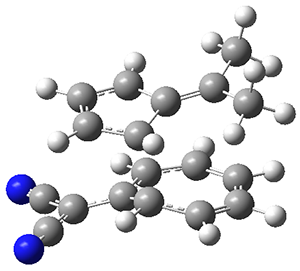
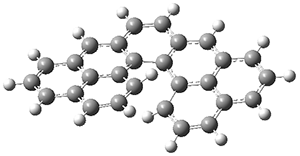
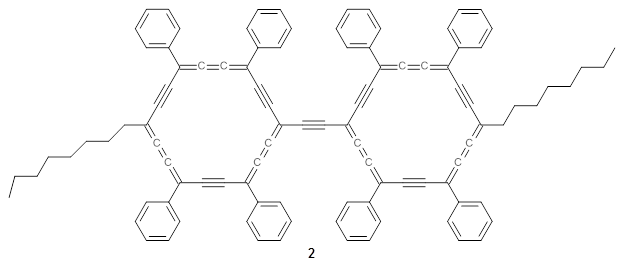
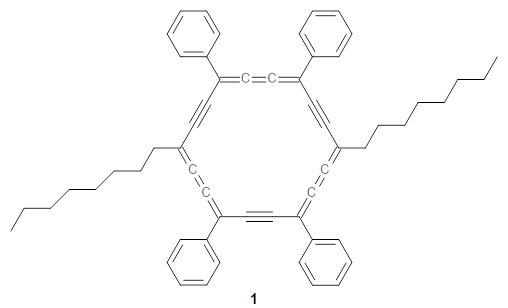
The authors test these two variants on 69 molecules. The original DP4 method predicted the correct stereoisomer for 75% of the examples, while dJ-DP4 correct identifies 96% of the cases. As a test of the indirect method, they examined marilzabicycloallenes A and B (1 and 2). DP4 predicts the correct stereoisomer with only 3.1% (1) or <0.1% (2) probability. dJ-DP4 predicts the correct isomer for 1 with 99.9% probability and 97.6% probability for 2. The advantage of iJ-DP4 is that using one coupling constant reduces the number of conformations that must be computed by 84%, yet maintains a probability of getting the correct assignment at 99.2% or better. Using two coupling constants to constrain conformations means that only 7% of all of the conformations need to be samples, and the predictive power is maintained.
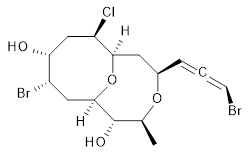
1 |
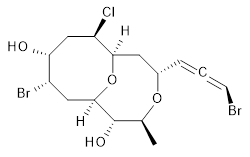 2 |
Both of these new methods clearly deserve further application.
References
1. Grimblat, N.; Gavín, J. A.; Hernández Daranas, A.; Sarotti, A. M., “Combining the Power of J Coupling and DP4 Analysis on Stereochemical Assignments: The J-DP4 Methods.” Org. Letters 2019, 21, 4003-4007, DOI: 10.1021/acs.orglett.9b01193.
InChIs
1: InChI=1S/C15H21Br2ClO4/c1-8-15(20)14-6-10(17)12(19)7-11(18)13(22-14)5-9(21-8)3-2-4-16/h3-4,8-15,19-20H,5-7H2,1H3/t2-,8-,9+,10-,11+,12+,13+,14+,15-/m0/s1
InChIKey=APNVVMOUATXTFG-NTSAAJDMSA-N
2: InChI=1S/C15H21Br2ClO4/c1-8-15(20)14-6-10(17)12(19)7-11(18)13(22-14)5-9(21-8)3-2-4-16/h3-4,8-15,19-20H,5-7H2,1H3/t2-,8-,9-,10-,11+,12+,13+,14+,15-/m0/s1
InChIKey=APNVVMOUATXTFG-SSBNIETDSA-N